一、数据的处理

1、插值

当题目中给出的数据有缺失时，可以通过插值的方法进行数据的填补。在matlab中有interp1(一维插值)、intero2(二维插值)、interp3(三维插值)等。

2、回归

回归分析是一种预测性的建模技术，它研究的是因变量和自变量之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。

3、拟合

根据已有数据进行未来一部分数据的预测。matlab中例如

p=ployfit(x,y,m),x,y为已知数据点向量的横纵坐标，m为拟合次数，返回m次拟合的系数赋予p
y0=polyval(p,x0)，求得多项式在x0处的值赋给y0

3.1 回归和拟合的区别

回归分析：是一种统计学上分析数据的方法，目的在于了解两个或多个变量间是否相关、相关方向与强度，并建立数学模型以便观察特定变量来预测研究者感兴趣的变量。

拟合：是一种把现有数据透过数学方法来代入一条数式的表示方式。如果你认同上面的两个定义的话。

回归分析包含的研究范围更多。拟合在某种程度上是承认了变量之间存在相关关系的，而回归则还要分析是否相关。所以可以把关系总结为：拟合是回归分析中分析变量相关方向与相关强度的一种方法

3.2 数据拟合的常用方法：最小二乘法

最小二乘法是由勒让德在19世纪发现的, 形式如下式:

$$ 目标函数=\sum(\text { 观测值 }-\text { 理论值 })^{2} $$

观测值就是我们的多组样本, 理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数, 我们的目标是得到使目标函数最小化时候的拟合函数的模型。举一个最简单的线性回归的简单例子, 比如我们有 $m$ 个只有一个特征的样本:

$$ \left(x_{i}, y_{i}\right)(i=1,2,3 \ldots, m) $$

样本采用一般的 $h_{\theta}(x)$ 为 $n$ 次的多项式拟合,

$$ h_{\theta}(x)=\theta_{0}+\theta_{1} x+\theta_{2} x^{2}+\ldots \theta_{n} x^{n}, \theta\left(\theta_{0}, \theta_{1}, \theta_{2}, \ldots, \theta_{n}\right) $$

最小二乘法就是要找到一组 $\theta\left(\theta_{0}, \theta_{1}, \theta_{2}, \ldots, \theta_{n}\right)$ 使得 $\sum_{i=1}^{n}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2}$ (残差平方和) 最小, 即求

$$ \min \sum_{i=1}^{n}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2} $$

对最小二乘法的理解可以参考这篇文章：

https://blog.csdn.net/ccnt_2012/article/details/81127117

最小二乘法的具体解法可以参考这篇文章：

https://blog.csdn.net/plm199513100/article/details/102873681

二、预测分析模型

1.灰色预测模型

1.1 基本信息

灰色系统介于黑色系统与白色系统之间，称部分信息已知、另部分信息未知，且内部各因素间有不确定的关系的系统为灰色系统。

灰色预测是通过少量的、不完全的信息，建立数学模型做出预测的一种预测方法。该方法基于客观事物的过去和现在的发展规律，对未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。其中GM(1,1)模型就是灰色预测中的强力工具之一。

该模型中，G表示Grey，M表示Model，括号中第一个1代表一阶微分方程，第二个1代表微分方程有一个变量。同理，灰色预测理论中GM(1,2)表示有两个变量的一阶微分方程灰色模型。

1.2 特点

原始数据必须等时间间距！！

GM(1.1)模型与统计模型相比,具有两个显著优点:

  1. 灰色模型即使在少量数据情况下建立的模型,精度也会很高.
  2. 灰色模型从其机理上讲,越靠近当前时间点精度会越高,因此灰色模型的预测功能优于统计模型。

灰色系统建模实际上是一种以数找数的方法,从系统的一个或几个离散数列中找出系统的变化关系,试图建立系统的连续变化模型。

2.马尔可夫链和马尔可夫模型

2.1 基本信息

要理解马尔可夫链首先需要知道随机过程，通俗地说，随机过程就是一些统计模型，利用这些统计模型可以对自然界的一些事物进行预测和处理。比如，在预测天气时，利用公式将下雨的概率计算出来，并进行预测。

马尔可夫链就是在知道当前状态分布和转移概率矩阵的情况下，利用当前状态对未来进行预测的过程。

比如：假设知道下雨后第二天晴天的概率和第二天阴天的概率，那么如果今天是雨天，就可以计算出明天是晴天和雨天的概率。

m阶马尔可夫模型的概念即：

状态间的转移仅依赖于前m个状态的过程，该过程就是m阶马尔可夫模型

如果该状态仅仅依赖于前一个状态, 这就是最简单的一阶马尔可夫模型:

$$ Pr\left(X_{n+1}=x \mid X_{1}=x_{1}, X_{2}=x_{2}, \ldots, X_{n}=x_{n}\right)=Pr\left(X_{n+1}=x \mid X_{n}=x_{n}\right) $$

对于马尔可夫模型的理解可以参考这篇文章

https://zhuanlan.zhihu.com/p/26453269

3.结合版：灰色-马尔可夫模型

3.1 基本信息

与灰色系统不同的是，马尔可夫模型则侧重于研究随机波动性较大的动态过程，根据状态之间的转移概率来预测系统未来的发展情况，因此能对随机波动序列进行长期预测。

其基本思想是：首先利用灰色GM(1,1)模型对预测的时间序列的发展趋势进行大致判断,然后用马尔可夫理论对预测结果进行精确的调整,这样可以使预测精度大幅度提高。

这是一个具体的基于灰色-马尔可夫模型的粮食年产量预测流程图举例：

基于灰色-马尔可夫模型的粮食年产量预测流程图.png

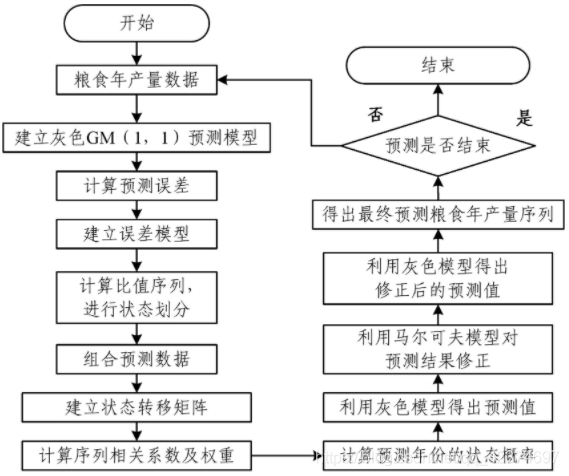
这个模型相关的资料不算特别多，可以参考一下这篇文章

https://blog.csdn.net/qq_42374697/article/details/111086335

4.时间序列的典型分解模型

4.1 基本信息

一个时间序列的典型分解式为：

$$ X_t=m_t+s_t+Y_t $$

其中$m_t$为趋势项，$s_t$是已知周期为d的周期项,$Y_t$是随机噪声项。

由于数据随时间的推移呈现出周期性的变化,因此我们可以根据周期对未来时间的数据进行预测。

具体内容见时间序列的典型分解模型.pdf

三、评价与决策类方法

1.层次分析法

1.1 基本信息

层次分析法(Analytic Hierarchy Process, AHP)是一种定量和定性相结合的、系统的、层次化的分析方法。这种方法的特点是在面对复杂问题的本质、影响因素和内在关系的基础上，利用较少的定量信息使决策的思维数学化，从而对多目标、多准则或无结构特性的复杂决策问题提供简单的决策方法。层次分析法是对无法完全定量的复杂系统做出决策的模型和方法。

1.2 具体步骤

  1. 建立层次结构模型；
  2. 构造判断矩阵；
  3. 层次单排序及其一致性检验；

  4. 层次总排序及一致性检验；

    层次分析法的基本步骤

    建立层次结构模型

    将决策的目标、考虑的因素(决策准则)和决策对象按他们之间的相互关系分成最高层、中间层和最低层，绘制层次结构图。

    1. 最高层(目标层)：决策的目的、要解决的问题；
    2. 中间层(准则层或指标层)：考虑的因素、决策的准则；
    3. 最低层(方案层)：决策时的备选方案；

    以旅游地为例进行分析：
    构建层次模型.png

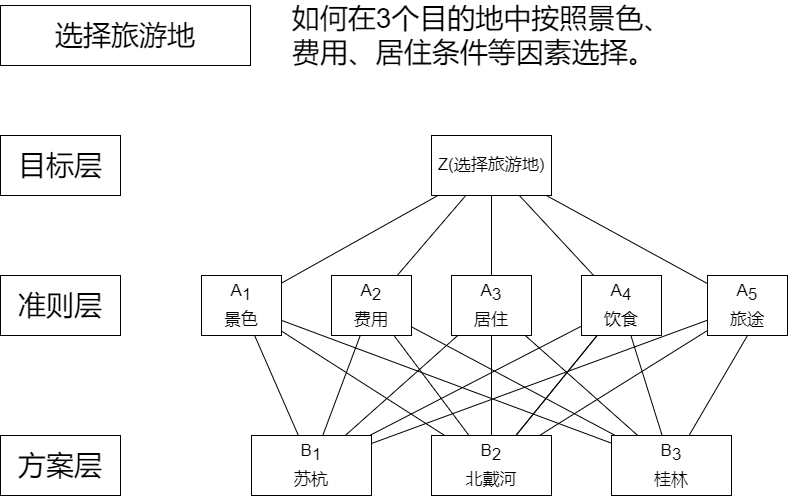
  5. 构造判断(成对比较)矩阵

    Santy等人提出一致矩阵法：

    1. 不把所有因素放在一起比较，而是两两比较；
    2. 采用相对尺度法，减少不同性质因素比较困难，提高准确率；

    $a_{ij}$表示第$i$个因素相对于第$j$个因素的比较结果，这个值使用Santy的1-9标度方法给出。

| 标度 | 含义（两个因素相比较） |
| :--------: | :-------------------------------------------------------------------------------------: |
| 1 | 具有同等重要性 |
| 3 | 一个因素比另一个因素稍微重要 |
| 5 | 一个因素比另一个因素明显重要 |
| 7 | 一个因素比另一个因素强烈重要 |
| 9 | 一个因素比另一个因素极端重要 |
| 2，4，6，8 | 相邻判断的中值 |
| 倒数 | 因素$i$与$j$比较的判断表示为$a_{ij}$，则因素$j$与$i$比较的判断$a_{ji}=\frac{1}{a_{ij}}$ |

  1. 层次单排序及一致性检验

    1. 一致性检验是指对成对比较矩阵确定不一致的允许范围。

      $$ \Lambda = \begin{bmatrix} 1&\frac{1}{2}&4&\Lambda\\ 2&1&7&\Lambda\\ \Lambda \end{bmatrix} $$

      矩阵中$a_{21}=2(C_{2}:C{1})$，$a_{13}=4(C1:C3)$可以得到$a_{23}=8(C_{2}:C_{3})$，与矩阵中的7不一致。在构造矩阵时很容易出现这种状况，这种不一致要在允许范围内。

      定义一致性指标：

      $$ CI=\frac{\lambda-n}{n-1} $$

      1. $CI=0$ ，有完全的一致性；
      2. $CI$ 接近于0，有满意的一致性；
      3. $CI$越大，不一致越严重；

      其中，n为矩阵的阶数，$\lambda$表示一致阵的最大特征根，满足$\lambda\ge n$。

      $$ RI=\frac{CI_{1}+CI_{2}+...+CI_{n}}{n}=\frac{\frac{\lambda_{1}+\lambda_{2}+...+\lambda_{n}}{n}-n}{n-1} $$

    随机一致性指标RI的数值:

| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| -- | - | - | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.41 | 1.45 | 1.49 | 1.45 | 1.51 |

定义一致性比率：$CR=\frac{CI}{RI}$

一般，当一致性比率$CR=\frac{CI}{RI}<0.1$时，认为$A$的不一致程度在容许的范围之内，有满意的一致性，通过一致性检验，可用其归一化特征向量作为权向量，否则要重新构造成对比较矩阵$A$，对$a_{ij}$加以调整。

#### 1.3 代码

A=[1 2 5 
    1/2 1 2
    1/5 1/2 1]
%% 一致性检验和权向量计算
n = length(A);
[v,d]=eig(A);%计算特征根和特征向量
[temp,loc] = max(max(d));%返回loc为特征向量所在列
r=max(max(d));
CI=(r-n)/(n-1);
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if  CR<0.10 || n==2
    CR_Result='通过';
else
    CR_Result='不通过';   
end

%% 权向量计算
w=v(:,loc)/sum(v(:,loc));
w=w';

%% 结果输出
disp('该判断矩阵权向量计算报告：');
disp(['CI:' num2str(CI)]);
disp(['CR:' num2str(CR)]);
disp(['一致性检验结果:' CR_Result]);
disp(['特征值:' num2str(r)]);
disp(['权向量:' num2str(w)]);

2.指标合成的客观权重方法

2.1 基本信息

通过计算每个指标的权重客观地对事物进行排名

2.2 准备工作

由于各个指标的取值范围不同，量纲与意义不同，为消除这些影响，需要对数据进行归一化处理。

2.3 客观权重确定的三种方法

熵权法

设 $\mathrm{n}$ 个学校的 $\mathrm{m}$ 个指标已经归一化处理, 数据为 $\mathrm{y}_{\mathrm{ij}}(\mathrm{i}=1,2, \ldots, \mathrm{n} ; \mathrm{j}=1,2, \ldots, \mathrm{m})$ 其第 $\mathrm{j}$ 项指标的信息熵计算公式为:

$$ \mathrm{E}_{\mathrm{j}}=-\frac{\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{p}_{\mathrm{ij}} \ln \mathrm{p}_{\mathrm{ij}}}{\ln \mathrm{n}} \quad \mathrm{j}=1,2, \cdots, \mathrm{m} $$

$0 \leq \mathrm{E}_{\mathrm{j}} \leq 1$ 其中 $\mathrm{p}_{\mathrm{ij}}=\frac{\mathrm{y}_{\mathrm{ij}}}{\sum_{\mathrm{i}=1}^{\mathrm{y}} \mathrm{y}_{\mathrm{ij}}}$, 若 $\mathrm{p}_{\mathrm{ij}}=0$, 则定义 $\mathrm{p}_{\mathrm{ij}} \ln \mathrm{p}_{\mathrm{ij}}=0$.
$\mathrm{E}_{\mathrm{j}}$ 越小，表明数据间差异越大, 因此提供的信息越大，该指标权重就越大
$\mathrm{E}_{\mathrm{j}}$ 越大, 表明数据间彼此越接近, 因此提供的信息越少, 该指标权重就越小
客观权重计算式:

$$ W_{j}=\frac{1-E_{j}}{m-\sum_{j=1}^{m} E_{j}} \quad j=1,2, \cdots, m $$

标准离差法

如果某个指标的标准差大, 因此提供的信息越大, 该指标权重就越大; 反之, 某个指标的标准差越小，因此提供的信息越少，该指标权重就越小。利用标准差来计算各指标的客观权重, 其计算式为

$$ W_{j}=\frac{\sigma_{j}}{\sum_{j=1}^{m} \sigma_{j}} \quad j=1,2, \cdots, m $$

CRITIC法确定权重

CRITIC法是Diakoulaki提出的一种客观赋权方法， 确定权值以两个基本概念为基础： 一是对比度，标准差越大权重相对越大。二是评价指标间的冲突性， 当两个指标间有较强的正相关，说明两个指标冲突性低，两个指标反映的信息具有较大的相似性；当两个指标间有较强的负相关，说明两个指标冲突性大， 两个指标反映的信息具有较大的不同。
确定第 $\mathrm{j}$ 个指标包含的信息量为: $\mathrm{c}_{\mathrm{j}}=\sigma_{\mathrm{j}} \sum_{\mathrm{i}=1}^{\mathrm{m}}\left(1-\mathrm{r}_{\mathrm{ij}}\right)(\mathrm{j}=1,2, \cdots, \mathrm{m})$

第 $\mathrm{j}$ 个指标权重为: $\mathrm{w}_{\mathrm{j}}=\frac{\mathrm{c}_{\mathrm{j}}}{\sum_{\mathrm{i}=1}^{\mathrm{m}} \mathrm{c}_{\mathrm{i}}}(\mathrm{j}=1,2, \cdots, \mathrm{m})$

具体内容见指标合成的客观权重方法.pdf

四、分类与判别类方法

1.聚类分析

1.1 基本信息

聚类分析是根据在数据中发现的描述对象及其关系的信息，将数据对象分组。目的是，组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内相似性越大，组间差距越大，说明聚类效果越好。

也就是说，聚类的目标是得到较高的簇内相似度和较低的簇间相似度，使得簇间的距离尽可能大，簇内样本与簇中心的距离尽可能小

2.判别分析

2.1 基本信息

根据观测到的样品的若干数量特征对样品进行归类、识别，判断其属性

3.主成分分析

3.1 基本信息

在实际问题研究中，多变量问题是经常会遇到的。变量太多，无疑会增加分析问题的难度与复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的。 因此，人们会很自然地想到，能否在相关分析的基础上，用较少的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来变量所反映的信息？

主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。

最后修改：2024 年 02 月 16 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏