似然

似然是给定某个参数值时，观察到当前数据的概率。对于参数 $\theta$ 和数据 $X$，似然函数可以表示为 $L(\theta | X)$，它是对数据的条件概率的函数。
形式：$L(\theta | X) = P(X | \theta)$

如下图，假设左边是理论世界，而右图是现实世界。假设我们知道理论上的概率，那么我们可以用来解释现实世界中正反面的情况。那么如果我们现在只观察到了现象，想要反过来求出理论中的概率值，那么就需要用到似然这个概念了。

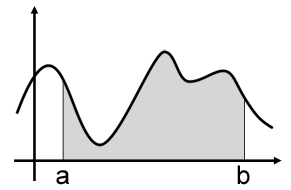
如图，我们根据右侧真实世界投十个币出现的正反值，其实可以推出好几种概率模型，但是他们哪种最接近真实的理论模型呢？还需要通过计算得出。也就是条件概率，举个例子。右侧真实世界十个硬币中7个是正面，3个是反面。那么如果按照左侧0.1，0.9的概率，就可以得出概率是 $0.1^7 *0.9^3$。这样算出来的每一个条件概率其实就是似然值，而极大似然估计其实就是想要求出似然值最大的模型，意味着距离真实模型最接近。

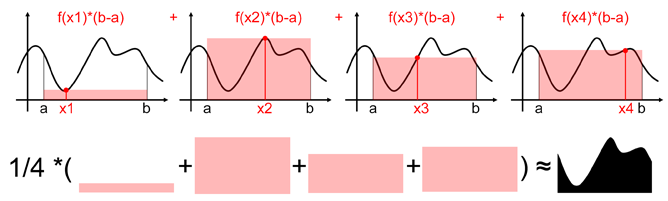
基本概念

极大似然估计的核心思想是：选择一组参数值，使得在这组参数下观测到当前样本的概率最大。

步骤

构建似然函数
对似然函数取对数（通常为了简化计算）
求导并令其等于零
解方程得到参数估计值

数学推导

$$ \begin{align*}P(x_1, x_2, x_3, x_4, ..., x_n \mid W, b) & = \prod_{i=1}^{n} P(x_i \mid W, b) \\ &= \prod_{i=1}^{n} P(x_i \mid y_i) \end{align*} $$

伯努利方程

$$ \text{其中：} x_i \in \{0, 1\};\\ f(x) = p^x (1-p)^{1-x} =\begin{cases} p, & x = 1 \\1 - p, & x = 0\end{cases} $$

$$ \begin{align*} &\log \left( \prod_{i=1}^{n} y_i^{x_i} (1 - y_i)^{1 - x_i} \right) \\ &= \sum_{i=1}^{n} \log \left( y_i^{x_i} (1 - y_i)^{1 - x_i} \right) \\ &= \sum_{i=1}^{n} \left( x_i \cdot \log y_i + (1 - x_i) \cdot \log (1 - y_i) \right) \\ \end{align*} $$

$$ \text{max} \left( \sum_{i=1}^{n} \left( x_i \cdot \log y_i + (1 - x_i) \cdot \log (1 - y_i) \right) \right) $$

$$ \text{min} \left( - \sum_{i=1}^{n} \left( x_i \cdot \log y_i + (1 - x_i) \cdot \log (1 - y_i) \right) \right) $$

为了便于计算，将其中取对数处理，但是最终目的还是求的最大似然值。习惯取最小值，因此常见形式是加负号取最小值。

极大似然估计