创建时间: 2024年11月5日 16:51
作者: 蜡笔大新
笔记类别: 强化学习
标签: Deep Reinforcement Learning, Policy Optimization, Reinforcement Learning
状态: 完成
基本原理
PG算法,全称为策略梯度算法(Policy Gradient Algorithm),是强化学习中的一种重要方法。它直接对策略进行优化,而不是通过值函数间接优化策略。这种方法在连续动作空间和高维动作空间中特别有效。
PG算法的核心思想是通过梯度上升的方式直接优化策略函数。它通过估计策略梯度来更新策略参数,使得期望回报最大化。这种方法允许智能体在每个状态下学习一个概率分布,用于选择最优动作。
之前提到的 Sarsa、Q-Learning 和 DQN 算法都是基于价值的方法,也就是先计算每个状态对应的动作的 Q 值,再选择 Q 值最大的动作执行。而 Policy Gradient 是一种更加直接的方式,它直接计算每个状态对应的动作的概率。这样做的优点就是它可以在一个连续区间内选取动作。
如果用一句话来表达策略梯度的直观解释,那就是“如果动作使得最终回报变大,那么增加这个动作出现的概率,反之,减少这个动作出现的概率”。这句话表达了两个含义:
- 我们考虑的是动作对于回报的影响,没有考虑状态或者其他因素。
- 我们调整的是动作出现的概率,而没有给某个动作打分,这区别于Value-based类的算法。
理解
PG算法不同于之前提到的基于价值类的算法,PG更多需要从整体和宏观网络的角度去理解。不再通过每个状态-动作对去更新,而是类似蒙特卡洛的思想,通过大量实验去逼近最终结果。总体的思路是:
- 从初始状态开始,按照当前策略选择动作,直到到达终止状态。这构成一条完整的轨迹。
- 从终止状态往回计算总的奖励和,作为这条路径的总奖励。
- 当完成了一定数量的路径后,将批量投入训练,具体则是梯度上升算法更新参数 $\theta$ ,目标是使总的期望奖励函数变得最大,从而得到最优策略。
我们将策略学习的目标函数定义为:
$$ J(\theta) = \mathbb{E}_{s_0}[V^{\pi_\theta}(s_0)] $$
核心公式
$$ \begin{align*}\nabla_\theta J(\theta) &\propto \sum_{s \in S} v^{\pi_\theta}(s) \sum_{a \in A} Q^{\pi_\theta}(s, a) \nabla_\theta \pi_\theta(a|s) \\&= \sum_{s \in S} v^{\pi_\theta}(s) \sum_{a \in A} \pi_\theta(a|s) Q^{\pi_\theta}(s, a) \frac{\nabla_\theta \pi_\theta(a|s)}{\pi_\theta(a|s)} \\&= \mathbb{E}_{\pi_\theta} [Q^{\pi_\theta}(s, a) \nabla_\theta \log \pi_\theta(a|s)]\end{align*} $$
解释:
- $\nabla_\theta J(\theta)$:这是目标函数$J(θ)$关于策略参数$θ$的梯度。
- $v^{\pi_\theta}(s)$:这是在状态$s$下,按照策略$π_θ$行动的值函数。
- $\nabla_\theta \pi_\theta(a|s)$:这是策略$π_θ$在状态$s$下选择动作$a$的概率关于参数$θ$的梯度。
- $\pi_\theta(a|s)$:这是在状态$s$下选择动作$a$的概率。
需要注意的是,因为上式中期望 $\mathbb{E}$ 的下标是 $\pi_\theta$ ,所以策略梯度算法为在线策略(on-policy)算法,即必须使用当前策略采样得到的数据来计算梯度。直观理解一下策略梯度这个公式,可以发现在每一个状态下,Q值越高则整个期望越大,因此可以认为梯度的修改是让策略更多地去采样到带来较高Q值的动作,更少地去采样到带来较低Q值的动作。
优势
PG算法具有以下优势:
- 适用于连续动作空间:不需要离散化动作空间,可以直接在连续空间中操作。
- 可以学习随机策略:这在某些环境中非常有用,特别是在部分可观察环境中。
- 收敛性好:在理论上,PG算法可以保证收敛到至少一个局部最优解。
代码
在CartPole-v0环境中,使用梯度策略方法中最基本的算法之一的REINFORCE算法训练模型。
import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import rl_utils
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class REINFORCE:
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
device):
self.policy_net = PolicyNet(state_dim, hidden_dim,
action_dim).to(device)
self.optimizer = torch.optim.Adam(self.policy_net.parameters(),
lr=learning_rate) # 使用Adam优化器
self.gamma = gamma # 折扣因子
self.device = device
def take_action(self, state): # 根据动作概率分布随机采样
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.policy_net(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
reward_list = transition_dict['rewards']
state_list = transition_dict['states']
action_list = transition_dict['actions']
G = 0
self.optimizer.zero_grad()
for i in reversed(range(len(reward_list))): # 从最后一步算起
reward = reward_list[i]
state = torch.tensor([state_list[i]],
dtype=torch.float).to(self.device)
action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
log_prob = torch.log(self.policy_net(state).gather(1, action))
G = self.gamma * G + reward
loss = -log_prob * G # 每一步的损失函数
loss.backward() # 反向传播计算梯度
self.optimizer.step() # 梯度下降
learning_rate = 1e-3
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = "CartPole-v0"
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = REINFORCE(state_dim, hidden_dim, action_dim, learning_rate, gamma,
device)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
transition_dict = {
'states': [],
'actions': [],
'next_states': [],
'rewards': [],
'dones': []
}
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done, _ = env.step(action)
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
state = next_state
episode_return += reward
return_list.append(episode_return)
agent.update(transition_dict)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()其中让我感到困惑的是update函数:
def update(self, transition_dict):
reward_list = transition_dict['rewards']
state_list = transition_dict['states']
action_list = transition_dict['actions']
G = 0
self.optimizer.zero_grad()
for i in reversed(range(len(reward_list))): # 从最后一步算起
reward = reward_list[i]
state = torch.tensor([state_list[i]],
dtype=torch.float).to(self.device)
action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
log_prob = torch.log(self.policy_net(state).gather(1, action))
G = self.gamma * G + reward
loss = -log_prob * G # 每一步的损失函数
loss.backward() # 反向传播计算梯度
self.optimizer.step() # 梯度下降明明PG算法使用的是梯度上升算法,为什么这里却是梯度下降。经过资料查阅,我了解到这其实是深度学习中一种常见的做法,loss = -log_prob * G 这一步其实就是在对损失函数取反,再进行梯度下降实际就相当于原来的梯度向上了,这样做法的原因在于很多优化器默认执行梯度下降,因此更加便捷使用标准优化器来实现梯度上升。
除了符号,还要乘对数概率log_prob的原因是:
- 它可以将乘法转换为加法,简化计算
- 它有助于数值稳定性,特别是在处理很小的概率时
- 它的梯度(即对数似然梯度)在数学上有良好的性质
结果
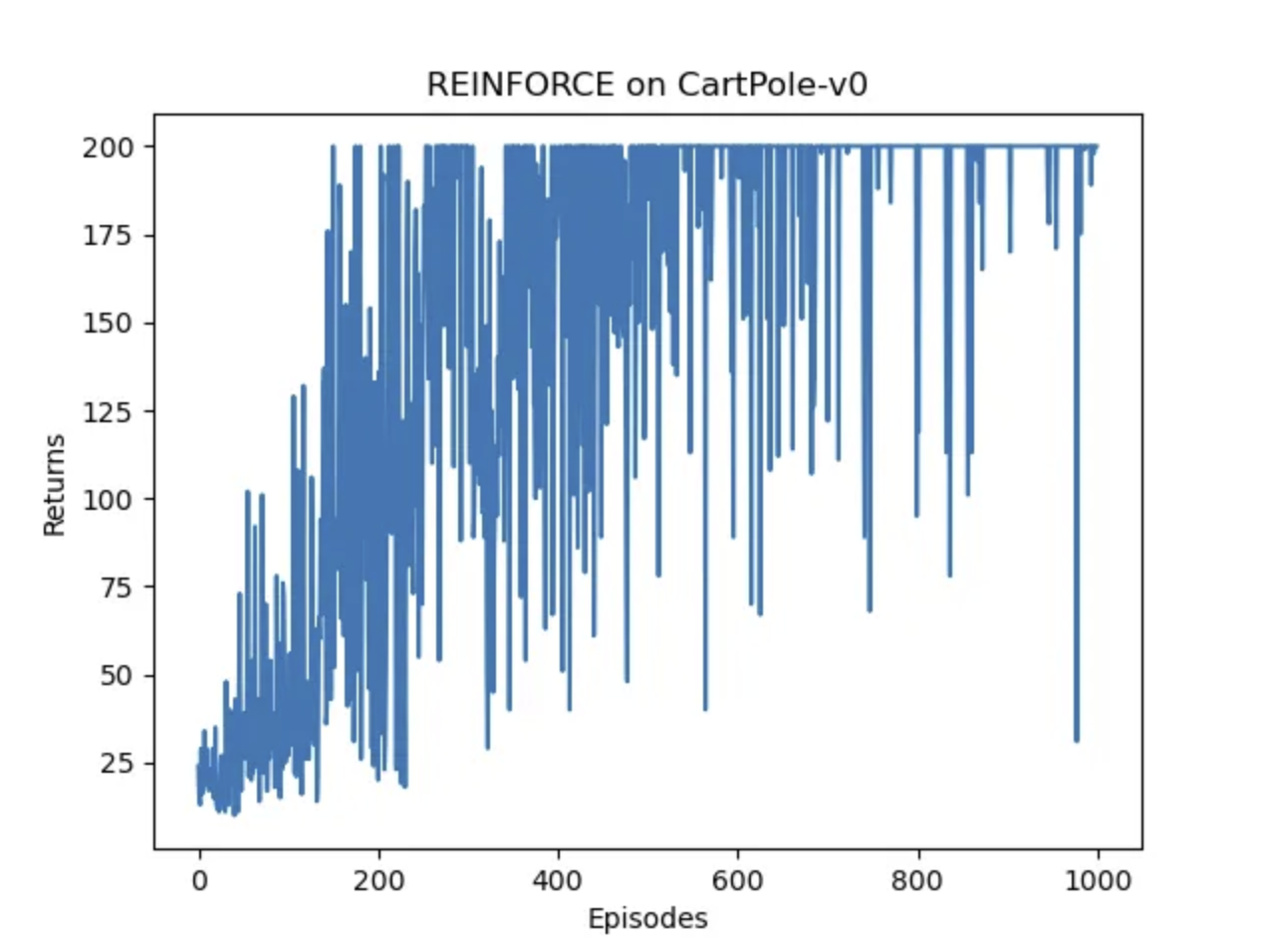
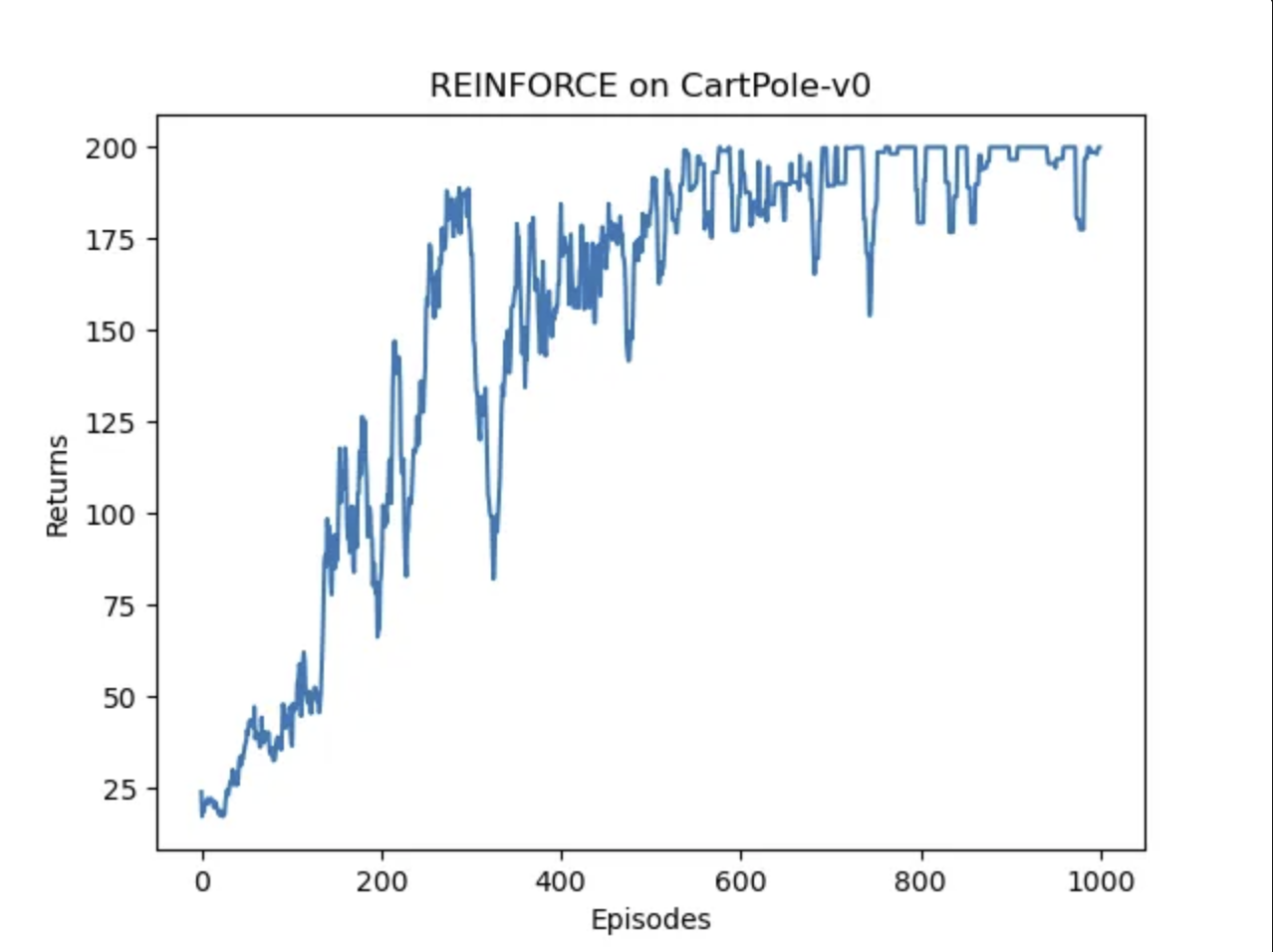
可以看出其实随着训练轮数的增长,回报有明显的增长,并且能够达到奖励和200的上限。