创建时间: 2024年10月23日 19:04
作者: 蜡笔大新
笔记类别: 强化学习
标签: Q-Learning, Reinforcement Learning, Temporal Difference Learning
状态: 完成
简介
TD算法，全称为"时间差分算法"（Temporal Difference Algorithm），是强化学习中的一种重要算法。它结合了动态规划和蒙特卡洛方法的优点，广泛应用于各种学习和决策问题。
核心思想
TD算法的核心思想是通过比较连续时间步骤的预测来学习。它使用当前估计和下一时间步的奖励来更新价值函数，而不需要等待整个序列完成。与其相反的蒙特卡洛方法，则是需要一直往前探索到结束，再往回走反馈奖励总和。
TD有点类似动态规划算法（DP），都利用状态转移方程（贝尔曼公式）。而区别主要在于，TD是不需要环境模型的，可以自由探索环境，不断用前方的奖励训练自身模型；而DP需要知道完整的模型，需要对整个状态空间进行迭代，DP方法在状态空间较大时计算代价高昂。
主要特点
- 在线学习：TD算法可以在每个时间步更新估计，无需等待整个序列结束。
- 自举：TD算法使用估计来更新估计，这种自举方法使其能够快速学习。
- 模型无关：TD算法不需要环境模型，可以直接从经验中学习。
变体
TD算法有多种变体，包括：
- Q-learning：一种off-policy TD控制算法
- SARSA：一种on-policy TD控制算法
- TD(λ)：结合了多步预测的TD算法
Q- Learning
在强化学习中，有两个核心概念：Q值和V值。Q值表示在某个状态下执行这个动作后，直到最终状态所获得的期望累积奖励；V值代表从这个状态开始，经过一系列决策到达最终状态的期望累积奖励。Q值和V值可以互相转化：一个状态的V值是其所有动作Q值的平均值；一个动作的Q值是下一个状态的V值加上当前动作的即时奖励。Q-learning是一种基于Q值的强化学习算法，主要思想是通过不断更新Q表来学习最佳策略。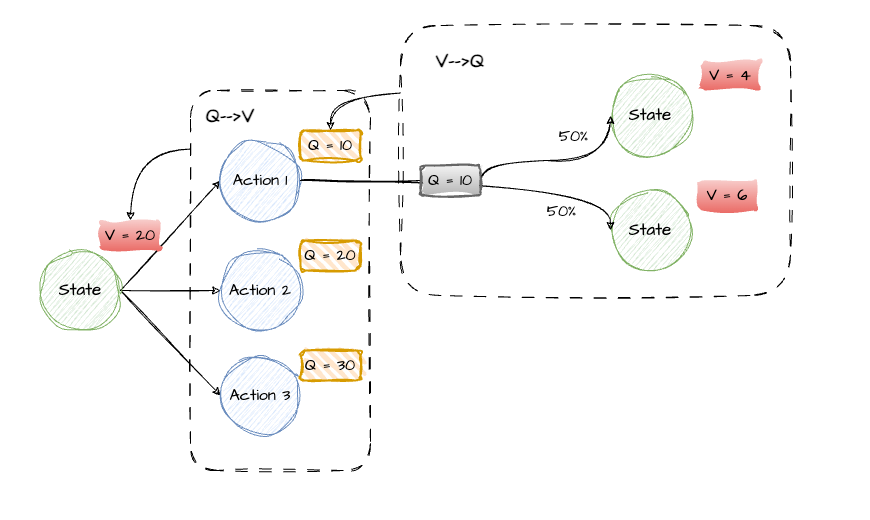
Q值
- 状态 (State, s): 系统或环境的当前状况。
- 动作 (Action, a): 在某个状态下，代理可以执行的行为选择。
- 奖励 (Reward, r): 执行某个动作后，代理从环境中获得的反馈信号，通常用于衡量该动作的好坏。
| Q-Table | a1 | a2 |
|---|---|---|
| s1 | q(s1,a1) | q(s1,a2) |
| s2 | q(s2,a1) | q(s2,a2) |
| s3 | q(s3,a1) | q(s3,a2) |
具体算法
每个“状态-动作对”都拥有自己的Q值，而Q-Learning的核心就是在于不断维护、更新这个Q-Table。
具体的算法步骤可以参考下图，主要步骤即为通过贪心算法更新 $[S_t, A_t]$状态-动作对下的q值，贪心算法是选取 $S_{t+1}$的状态下Q值最大的动作，利用奖励R反推。递推公式为贝尔曼公式：
$$ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_t + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t) \right] $$
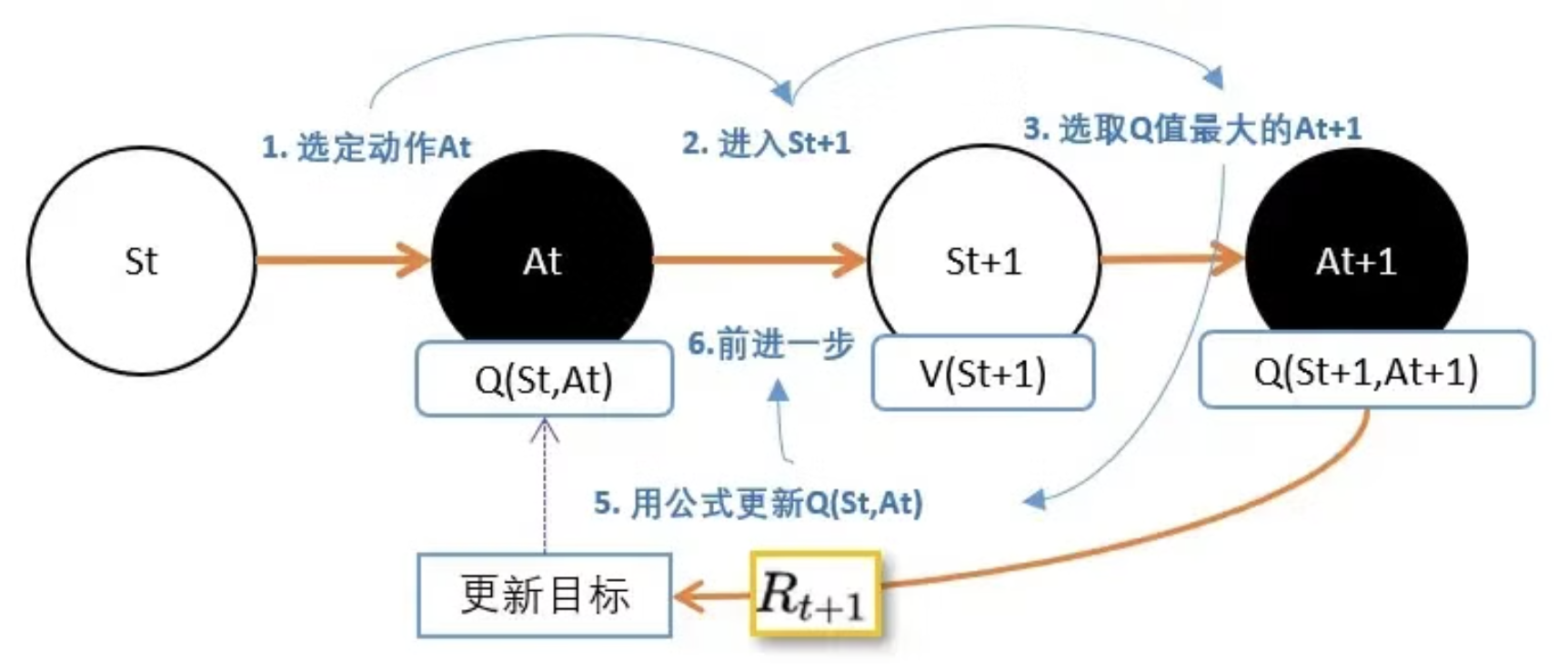
其中：
- $s_t$ 是当前状态
- $a_t$ 是当前动作
- $r_t$ 是在执行动作后获得的奖励
- $s_{t+1}$ 是下一个状态
- $a'$ 是未来可能的动作
- $\alpha$ 是学习率（Learning Rate），控制每次更新Q值的步长。
- $\gamma$ 是折扣因子（Discount Factor），表示未来奖励的权重（0到1之间的数）。高 $\gamma$ 值意味着未来奖励更重要。
当初始化时，Q-Table所有Q值都为0，更新的时候会直接用奖励值。
Sarsa
Sarsa与Q-Learning很相似，区别是：
- Q-Learning选取的是下一个状态下最大Q值的动作；而Sarsa选取的仍是前一个动作，即 $A_t$ 。
- Q-learning是一种离线策略（off-policy）算法，它学习的是最优策略，不管当前正在执行的是什么策略，因此更倾向于探索；Sarsa是一种在线策略（on-policy）算法，它学习的是当前正在执行的策略，因此更保守。
举例
| 状态 (State) \动作（Action） | 动作A1 | 动作A2 |
|---|---|---|
| S1 | 5 | 9 |
| S2 | 3 | 2 |
| S3 | 7 | 1 |
通过上述Q表，我们可以清晰的看出在每个状态下采取不同动作的奖励期望值，我们只需要在每个状态下选取收益最大的动作即可。
代码
环境
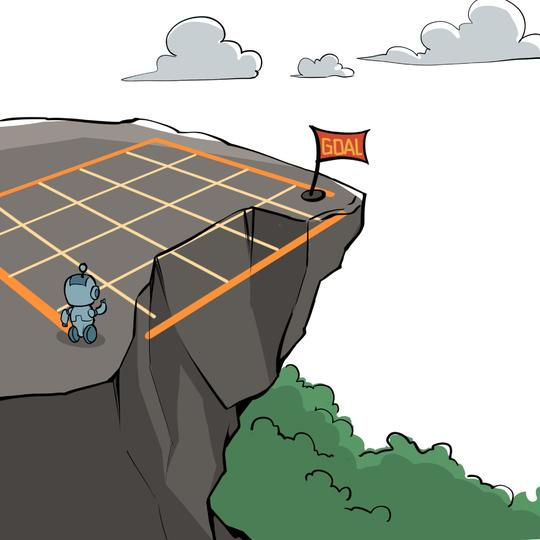
悬崖漫步环境要求一个智能体从起点出发，避开悬崖行走，最终到达目标位置。
智能体在每一个状态都可以采取 4 种动作：上、下、左、右。如果智能体采取动作后触碰到边界墙壁则状态不发生改变，否则就会相应到达下一个状态。环境中有一段悬崖，智能体掉入悬崖或到达目标状态都会结束动作并回到起点，也就是说掉入悬崖或者达到目标状态是终止状态。智能体每走一步的奖励是 −1，掉入悬崖的奖励是 −100。
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm # tqdm是显示循环进度条的库
class CliffWalkingEnv:
def __init__(self, ncol, nrow):
self.nrow = nrow
self.ncol = ncol
self.x = 0 # 记录当前智能体位置的横坐标
self.y = self.nrow - 1 # 记录当前智能体位置的纵坐标
def step(self, action): # 外部调用这个函数来改变当前位置
# 4种动作, change[0]:上, change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)
# 定义在左上角
change = [[0, -1], [0, 1], [-1, 0], [1, 0]]
self.x = min(self.ncol - 1, max(0, self.x + change[action][0]))
self.y = min(self.nrow - 1, max(0, self.y + change[action][1]))
next_state = self.y * self.ncol + self.x
reward = -1
done = False
if self.y == self.nrow - 1 and self.x > 0: # 下一个位置在悬崖或者目标
done = True
if self.x != self.ncol - 1:
reward = -100
return next_state, reward, done
def reset(self): # 回归初始状态,坐标轴原点在左上角
self.x = 0
self.y = self.nrow - 1
return self.y * self.ncol + self.x
def print_agent(agent, env, action_meaning, disaster=[], end=[]):
for i in range(env.nrow):
for j in range(env.ncol):
if (i * env.ncol + j) in disaster:
print('****', end=' ')
elif (i * env.ncol + j) in end:
print('EEEE', end=' ')
else:
a = agent.best_action(i * env.ncol + j)
pi_str = ''
for k in range(len(action_meaning)):
pi_str += action_meaning[k] if a[k] > 0 else 'o'
print(pi_str, end=' ')
print()
class QLearning:
""" Q-learning算法 """
def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
self.Q_table = np.zeros([nrow * ncol, n_action]) # 初始化Q(s,a)表格
self.n_action = n_action # 动作个数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略中的参数
def take_action(self, state): #选取下一步的操作
if np.random.random() < self.epsilon:
action = np.random.randint(self.n_action)
else:
action = np.argmax(self.Q_table[state])
return action
def best_action(self, state): # 用于打印策略
Q_max = np.max(self.Q_table[state])
a = [0 for _ in range(self.n_action)]
for i in range(self.n_action):
if self.Q_table[state, i] == Q_max:
a[i] = 1
return a
def update(self, s0, a0, r, s1):
td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]
self.Q_table[s0, a0] += self.alpha * td_error
class Sarsa:
""" Sarsa算法 """
def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
self.Q_table = np.zeros([nrow * ncol, n_action]) # 初始化Q(s,a)表格
self.n_action = n_action # 动作个数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略中的参数
def take_action(self, state): # 选取下一步的操作,具体实现为epsilon-贪婪
if np.random.random() < self.epsilon:
action = np.random.randint(self.n_action)
else:
action = np.argmax(self.Q_table[state])
return action
def best_action(self, state): # 用于打印策略
Q_max = np.max(self.Q_table[state])
a = [0 for _ in range(self.n_action)]
for i in range(self.n_action): # 若两个动作的价值一样,都会记录下来
if self.Q_table[state, i] == Q_max:
a[i] = 1
return a
def update(self, s0, a0, r, s1, a1):
td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]
self.Q_table[s0, a0] += self.alpha * td_error
ncol = 12
nrow = 4
env = CliffWalkingEnv(ncol, nrow)
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
agent = Sarsa(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500 # 智能体在环境中运行的序列的数量
return_list = [] # 记录每一条序列的回报
for i in range(10): # 显示10个进度条
# tqdm的进度条功能
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)): # 每个进度条的序列数
episode_return = 0
state = env.reset()
action = agent.take_action(state)
done = False
while not done:
next_state, reward, done = env.step(action)
next_action = agent.take_action(next_state)
episode_return += reward # 这里回报的计算不进行折扣因子衰减
agent.update(state, action, reward, next_state, next_action)
state = next_state
action = next_action
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
action_meaning = ['^', 'v', '<', '>']
print('Sarsa算法最终收敛得到的策略为：')
print_agent(agent, env, action_meaning, list(range(37, 47)), [47])
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Sarsa on {}'.format('Cliff Walking'))
plt.show()
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
agent = QLearning(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500 # 智能体在环境中运行的序列的数量
return_list = [] # 记录每一条序列的回报
for i in range(10): # 显示10个进度条
# tqdm的进度条功能
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)): # 每个进度条的序列数
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done = env.step(action)
episode_return += reward # 这里回报的计算不进行折扣因子衰减
agent.update(state, action, reward, next_state)
state = next_state
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Q-learning on {}'.format('Cliff Walking'))
plt.show()
action_meaning = ['^', 'v', '<', '>']
print('Q-learning算法最终收敛得到的策略为：')
print_agent(agent, env, action_meaning, list(range(37, 47)), [47])结果
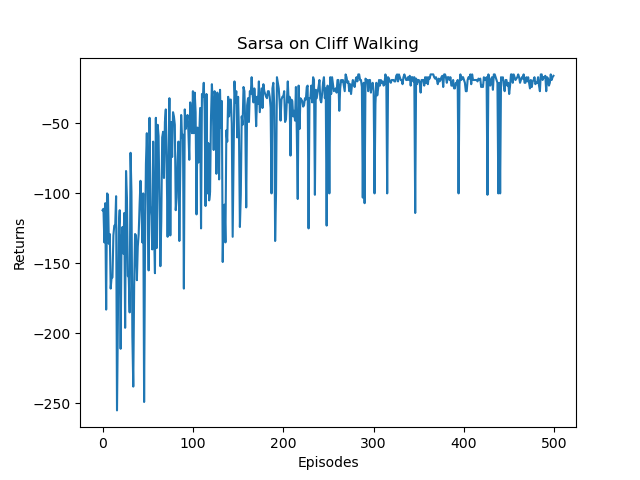
Sarsa：
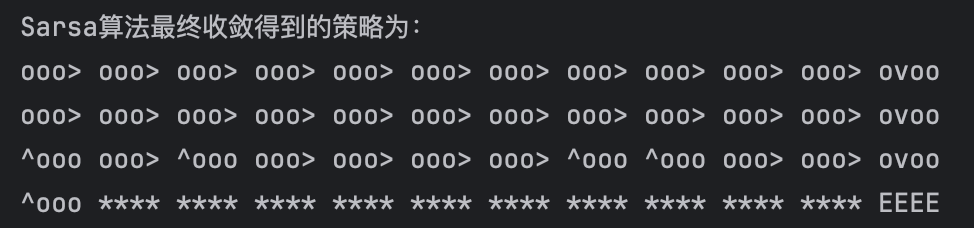
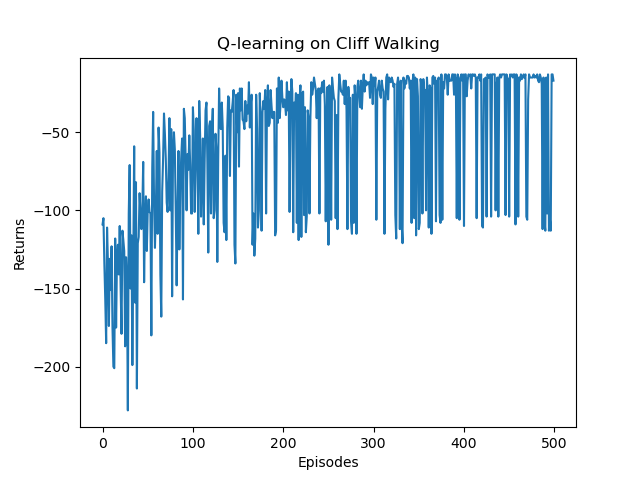
Q-Learning
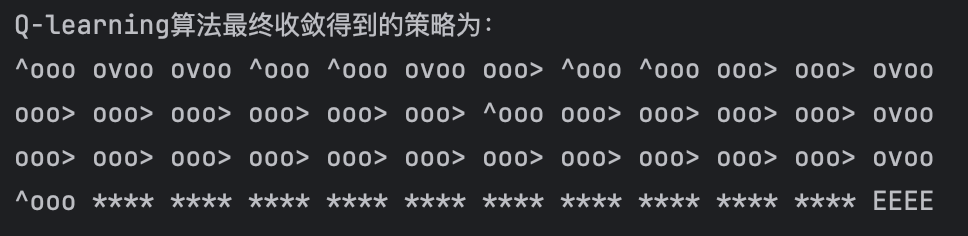
打印出来的动作，我们用^o<o表示等概率采取向左和向上两种动作，ooo>表示在当前状态只采取向右动作。
通过Sarsa和Q-Learning结果的对比，可以比较明显的看出Sarsa和Q-Learning都能比较好的学习到策略，奖励逐步上升，最后到达终点。Sarsa比Q-Learning更稳定一些，没有非常大的起伏。通过路线图可以看出，Sarsa更加保守，偏向于在更安全的地方行走，Q-Learning更加偏向于探索，能够在悬崖边上行走。正因如此，Q-Learning更加容易掉入悬崖，这在奖励图上也有所体现。
