创建时间: 2024年10月29日 18:21
作者: 蜡笔大新
笔记类别: 强化学习
标签: Markov Chain, Markov Property
状态: 完成
马尔可夫性质(Markov Property)
马尔可夫性质是这些概念的核心,也是最基础的概念。它表明:一个过程的未来状态只依赖于当前状态,而与之前的状态无关。
数学上,如果一个过程满足马尔可夫性质,那么对于任何时刻 $t$ ,有:
$$ P(s_{t+1} | s_t, s_{t-1}, \dots, s_0) = P(s_{t+1} | s_t) $$
这就是说,给定当前状态 $s_t$ ,下一个状态 $s_{t+1}$ 的概率分布不依赖于更早的状态 $s_{t-1}, \dots, s_0$ 。马尔可夫性质是一种“无记忆性”,强调当前状态已包含了做决策所需的所有信息。
马尔可夫链(Markov Chain)
马尔可夫链是一种描述随机过程的数学模型,满足马尔可夫性质的一种特殊的离散时间、离散状态的随机过程。
基本概念
• 状态空间:马尔可夫链中的所有可能状态的集合。
• 转移概率:从一个状态转移到另一个状态的概率。
• 转移矩阵:一个矩阵,描述了所有状态之间的转移概率。
转移矩阵
假设状态空间为 $S = \{s_1, s_2, \dots, s_n\}$ ,则转移矩阵 P 为:
$$ P = \begin{bmatrix}P(s_1 \to s_1) & P(s_1 \to s_2) & \cdots & P(s_1 \to s_n) \\P(s_2 \to s_1) & P(s_2 \to s_2) & \cdots & P(s_2 \to s_n) \\\vdots & \vdots & \ddots & \vdots \\P(s_n \to s_1) & P(s_n \to s_2) & \cdots & P(s_n \to s_n)\end{bmatrix} $$
其中 $P(s_i \to s_j)$ 表示从状态 $s_i$ 转移到状态 $s_j$ 的概率。
从某个状态出发,到达其他状态的概率和必须为 1,即状态转移矩阵$P$的每一行的和为 1。
举例:
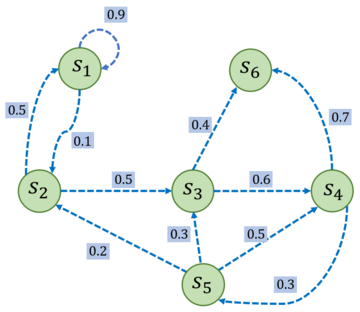
$P$ 矩阵为:
$$ \mathcal{P} = \begin{bmatrix}0.9 & 0.1 & 0 & 0 & 0 & 0 \\0.5 & 0 & 0.5 & 0 & 0 & 0 \\0 & 0 & 0.6 & 0 & 0.4 & 0 \\0 & 0 & 0 & 0.3 & 0.7 & 0 \\0 & 0.2 & 0.3 & 0.5 & 0 & 0 \\0 & 0 & 0 & 0 & 0 & 1 \\\end{bmatrix} $$
马尔可夫过程(Markov Process)
马尔可夫过程有时与马尔可夫链互换使用,但更广义地指满足马尔可夫性质的过程。它们可以是离散或连续状态、离散或连续时间的随机过程。
从定义上看:
- 马尔可夫链是马尔可夫过程的一种特例,即离散状态和离散时间的马尔可夫过程。
- 广义的马尔可夫过程可以是连续状态和时间的。
离散例子:在一个天气模型中,如果今天的天气状态是晴天,那么明天的天气状态转为雨天或继续晴天的概率取决于今天的状态,而与之前的天气无关。
连续例子:在一个股票模型中,股票价格的变化可以被视为一个连续的马尔可夫过程。在任何给定时刻,股票的未来价格只依赖于其当前价格,而不直接依赖于过去的价格变动。这种模型假设市场是有效的,所有相关的历史信息都已反映在当前价格中。
当前状态是未来的充分统计量,即下一个状态只取决于当前状态,而不会受到过去状态的影响。需要明确的是,具有马尔可夫性并不代表这个随机过程就和历史完全没有关系。因为虽然时刻 $t+1$
的状态只与时刻 $t$ 的状态有关,但是时刻 $t$ 的状态其实包含了时刻 $t-1$ 的状态的信息,通过这种链式的关系,历史的信息被传递到了现在。马尔可夫性可以大大简化运算,因为只要当前状态可知,所有的历史信息都不再需要了,利用当前状态信息就可以决定未来。
例子2

假设这个 $P$ 矩阵是时齐的,也就是说随着时间推移,概率是不变的。那么第二天计算第三天的概率矩阵仍然是这个矩阵 $P$ 。那么第二天的概率也就是 第一天的概率矩阵 $ \times P$ ;第三天的概率即 第二天的概率矩阵 $ \times P$,以此类推。我们就可以计算出第N天的概率矩阵。
再以这个例子理解一下马尔可夫过程。第N天吃饭睡觉玩耍的概率,其实是由第N-1天的概率矩阵计算得来的,因此可以理解只与上一个状态有关,但是实际上包含了过去的每一个状态的信息。

马尔可夫决策过程(Markov Decision Process, MDP)
定义
马尔可夫决策过程是在马尔可夫过程的基础上加入了决策和奖励的概念。在强化学习中,MDP 是描述决策问题的数学模型,它由以下四个部分构成:
- 状态集合 $S$ :代表环境的所有可能状态。
- 动作集合 $A$ :代表智能体可以选择的所有可能动作。
- 转移概率 $P(s{\prime} | s, a)$ :智能体在状态 $s$ 下执行动作 $a$ 后转移到状态 $s{\prime}$ 的概率。
- 奖励函数 $R(s, a)$ :智能体在状态 $s$ 下执行动作 $a$ 后获得的即时奖励。
转移概率 $P$ 举例:用来描述一些具有不确定性问题的概率,例如打羽毛球可能会由于刮风而发生角度偏移,例如30%向左偏,40%向前,30%向右偏。这个概率和之前的状态没有关系,只与当前状态有关,因此符合马尔可夫决策过程。转移概率在理论上用于评估策略,而实际编码中,经常不用考虑具体的转移概率,而是考虑拥有的可能性并构建相应奖励函数。
累积奖励(折扣回报)
在强化学习中,智能体不仅关注即时奖励 $R(s, a)$ ,更注重长期累积奖励 $G_t$ ,其定义为从当前时刻 $t$ 开始累积的未来奖励之和。引入一个折扣因子 $\gamma \in [0, 1]$ 控制未来奖励的影响,累积奖励公式为:
$$ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} $$
累积奖励关注的是从当前状态通过指定路径到达目标状态的奖励之和。
与Q值的区别在于:
- Q值关注当前状态执行某个动作获得的奖励期望
- 累积奖励关注按照这个策略(路径)一共能获得多少奖励
公式中,越靠近当前状态,权重越大;越远离当前状态,权重越小(通过 $\gamma$ 的次方控制)。
- 当 $\gamma$ 接近 1 时,智能体会更加重视远期奖励,愿意为长期的回报做出权衡。
- 当 $\gamma$ 较小时,智能体会更加关注近期的回报,对较远的奖励不太重视。
总结
| 概念 | 解释 | 是否有决策、奖励 |
|---|---|---|
| 马尔可夫性质 | 当前状态决定未来状态,与历史无关 | 否 |
| 马尔可夫链 | 离散时间、离散状态的马尔可夫过程 | 否 |
| 马尔可夫过程 | 广义的满足马尔可夫性质的过程 | 否 |
| 马尔可夫决策过程 (MDP) | 带有决策和奖励的马尔可夫过程 | 是 |
