创建时间: 2024/12/2 12:45:16
作者: 蜡笔大新
笔记类型: 强化学习
简介
DDPG(Deep Deterministic Policy Gradient)是一种基于 Actor-Critic 结构的深度强化学习算法。传统的 Q-Learning 只能处理离散状态和动作,DQN 能处理连续状态和离散动作,而DDPG则解决了在连续状态和动作空间下的强化学习问题。DDPG 与梯度策略算法系列中的 REINFORCE 算法有所不同:REINFORCE 提供随机策略,而 DDPG 提供确定性策略(Deterministic Policy)。具体来说,非确定性策略 $\pi_\theta$ 输出每个动作的概率(对于连续动作则是概率分布曲线),可以通过 $\epsilon$ 策略或选择最高概率的动作来决策;而确定性策略则直接输出具体动作,记作 $a=\mu_\theta (s)$。由于 DDPG 的确定性特征限制了其探索能力,因此算法中添加了随机噪声来增强探索。
网络
Actor
与传统 Actor-Critic 算法中的 Actor 类似,DDPG 中的 Actor 也是一个神经网络,区别在于神经网络和激活函数的设置不一样。DDPG 的 Actor 通常最后一层直接输出一个具体值,对于连续动作空间,可能会使用特定的激活函数限制输出范围,例如:
- Tanh 激活函数:限制输出在 [-1, 1]。
- 线性输出:直接输出在连续范围内的值。
最后会输出一个网络认为的价值期望最高的动作,输出维度等于动作空间的维度。
Critic
DDPG 的 Critic 网络与 DQN 的 Q 网络和传统 AC 的 Critic 网络有明显区别。DQN 的 Q 网络输入状态后输出所有动作的 Q 值,这种方式只适用于离散动作问题,无法处理连续动作空间。传统 AC 算法中的 Critic 使用神经网络来估计状态的 V 值。而 DDPG 的 Critic 则采用神经网络同时接收状态和动作作为输入,用于预估 Q 值。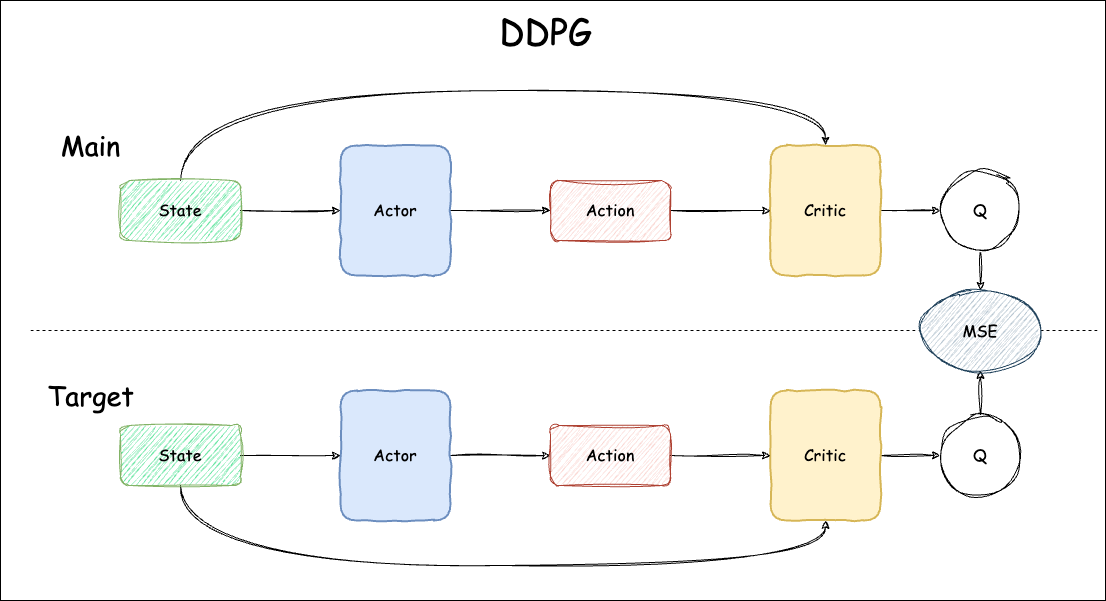
更新
网络参数更新的时间节点主要是在经验池满了之后,随机采样经验池的经验进行更新,通过这种机制能够有效减少样本的时间相关性,避免模型过度依赖于某些特定的样本,使得训练数据更具多样性,增强了策略在不同场景中的泛化能力,提升模型的训练稳定性。
Actor
Actor 网络主要使用神经网络输出当前状态下价值期望最高的动作,其优化的目标就是最大化 Critic 网络的 Q 值,更新主要是通过 Critic 网络输出的 Q 值进行梯度上升。
Critic
Critic 网络的损失函数是当前 Q 值和目标 Q 值的[[均方误差(MSE)]]。其更新目标是最小化这个均方误差,通过梯度下降来更新参数。
MSE公式
$$ L(\theta^Q) = \frac{1}{N} \sum_{i=1}^N \left( Q_{\text{target}, i} - Q(s_i, a_i|\theta^Q) \right)^2 $$
目标 Q 值的计算
$$ Q_{\text{target}, i} = r_i + \gamma (1 - \text{done}_i) Q'(s'_i, \mu'(s'_i|\theta^{\mu'})|\theta^{Q'}) $$
这个公式其实就是贝尔曼公式的变种。
其中:
$Q_{\text{target}, i}$ 表示目标网络的 Q 值。从当前状态 $s_i$ 和动作 $a_i$ 开始,未来累积奖励的估计值。
$r_i$ 表示智能体在当前状态 $s_i$ 执行动作 $a_i$ 后,从环境中获得的奖励
$\gamma$ 表示折扣因子
$done_i$ 表示当前状态是否是终止状态(0代表未终止,1代表终止)
$\mu'(s'_i|\theta^{\mu'})$ 代表目标 Actor 网络根据 $\theta^{Q'}$ 软更新参数 $\theta^{Q}$ 的情况下,根据下一个状态 $s'_i$ 生成的动作
$Q{\prime}(s{\prime}_i, a{\prime}|\theta^{Q{\prime}})$ 表示目标 Critic 网络根据下一个状态和下一个动作生成的 Q 值
至此,重新梳理一下整个目标 Q 值的计算:
- 获取当前状态 $s_t$ 和当前动作 $a_t$
- 当前状态 $s_t$ 执行当前动作 $a_t$,获取下一个状态 $s_{t+1}$
- 将下一个状态 $s_{t+1}$ 输入进目标 Actor 网络,获取下一个动作 $a_{t+1}$
- 将下一个状态 $s_{t+1}$ 和下一个动作 $a_{t+1}$ 输入进目标 Critic 网络,获取 Q 值
- 将目标 Critic 网络生成的 Q 值与折扣因子、完成状态、当前状态 $s_t$ 执行当前动作 $a_t$ 获得的奖励一起代入公式计算目标 Q 值
软更新
软更新一般是在随机采样更新完当前 Actor 和 Critic 网络后,对两个目标网络利用公式进行的。由于参数的设置,其实际效果就是每次只更新当前网络的非常小的部分,绝大多数都还是由原来的目标网络参数构成。
$$ \theta^{Q'} \leftarrow \tau \theta^Q + (1 - \tau) \theta^{Q'} $$
$$ \theta^{\mu'} \leftarrow \tau \theta^\mu + (1 - \tau) \theta^{\mu'} $$
其中:
$\theta^{Q{\prime}}$:目标 Critic 网络的参数
$\theta^{Q}$:当前 Critic 网络的参数
$\theta^{\mu{\prime}}$:目标 Actor 网络的参数
$\theta^{\mu}$:当前 Actor 网络的参数
$\tau$:软更新系数,通常取值很小(如 $\tau$ = 0.001)
其它亮点
归一化
在 DDPG 的原版论文中,提到了批量归一化。
批量归一化有助于减小训练中的 协方差偏移(covariance shift),确保每一层接收到归一化的输入数据。在低维情况下,批量归一化被应用于状态输入、策略网络的所有层,以及价值网络中动作输入之前的所有层。
使用批量归一化后,可以跨不同任务(任务特征和单位类型不同)进行有效学习,而无需手动调整特征范围。
噪声
在 DDPG 的原版论文中,提到了添加噪声来增加探索性。由于 DDPG 的 Actor 网络输出的是确定性动作,因此不能像以往的 DQN 一样通过 $\epsilon$ 贪婪策略来探索。原文采用的是Ornstein-Uhlenbeck 噪声,这是一种时间相关的噪声,用于在具有惯性的物理控制问题中提升探索效率。
在这个公式中,主要是对 Actor 网络生成的动作添加一些随机的噪声 $N$ 来干扰,在解决连续动作时效果比较显著。解决连续动作时一般输出一个数值,例如机器人的手臂转动角度,通过添加噪声可以更好的实现探索效果。
$$ \mu'(s_t) = \mu(s_t \mid \theta_t^\mu) + \mathcal{N} $$
总体流程
DDPG 的训练总体流程主要分为交互、更新,分别在上文进行了阐述。
- 大部分时间里,网络中的智能体与环境进行交互,获得奖励、动作等状态,产生经验,将经验放在经验池里。
- 当经验池满了之后,取出部分经验开始更新。
- 使用 MSE 作为 Critic 的损失函数,计算当前 Q 值和目标 Q 值的误差,并用这个误差梯度下降更新 Critic 的参数。
- 使用 Critic 的 Q 值梯度上升更新 Actor 的参数。
- 利用软更新公式对目标 Actor 网络和目标 Critic 网络进行软更新。
- 若未训练完成则继续与环境交互。
总体流程图如下:
优缺点分析
优点
- 适用于连续动作空间
- 样本效率较高
- 结合了值函数和策略梯度方法的优势
缺点
- 对超参数较为敏感
- 训练不够稳定
- 可能存在过估计问题
代码
import random
import gym
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
self.action_bound = action_bound # action_bound是环境可以接受的动作最大值
def forward(self, x):
x = F.relu(self.fc1(x))
return torch.tanh(self.fc2(x)) * self.action_bound
class QValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
self.fc_out = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1) # 拼接状态和动作
x = F.relu(self.fc1(cat))
x = F.relu(self.fc2(x))
return self.fc_out(x)
class DDPG:
""" DDPG算法 """
def __init__(self, state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
# 初始化目标价值网络并设置和价值网络相同的参数
self.target_critic.load_state_dict(self.critic.state_dict())
# 初始化目标策略网络并设置和策略相同的参数
self.target_actor.load_state_dict(self.actor.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.sigma = sigma # 高斯噪声的标准差,均值直接设为0
self.tau = tau # 目标网络软更新参数
self.action_dim = action_dim
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.actor(state).item()
# 给动作添加噪声,增加探索
action = action + self.sigma * np.random.randn(self.action_dim)
return action
def soft_update(self, net, target_net):
for param_target, param in zip(target_net.parameters(), net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
next_q_values = self.target_critic(next_states, self.target_actor(next_states))
q_targets = rewards + self.gamma * next_q_values * (1 - dones)
critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), q_targets))
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
actor_loss = -torch.mean(self.critic(states, self.actor(states)))
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
self.soft_update(self.actor, self.target_actor) # 软更新策略网络
self.soft_update(self.critic, self.target_critic) # 软更新价值网络
actor_lr = 3e-4
critic_lr = 3e-3
num_episodes = 1000
hidden_dim = 64
gamma = 0.98
tau = 0.005 # 软更新参数
buffer_size = 10000
minimal_size = 1000
batch_size = 64
sigma = 0.01 # 高斯噪声标准差
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'Pendulum-v1'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0] # 动作最大值
agent = DDPG(state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device)
return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
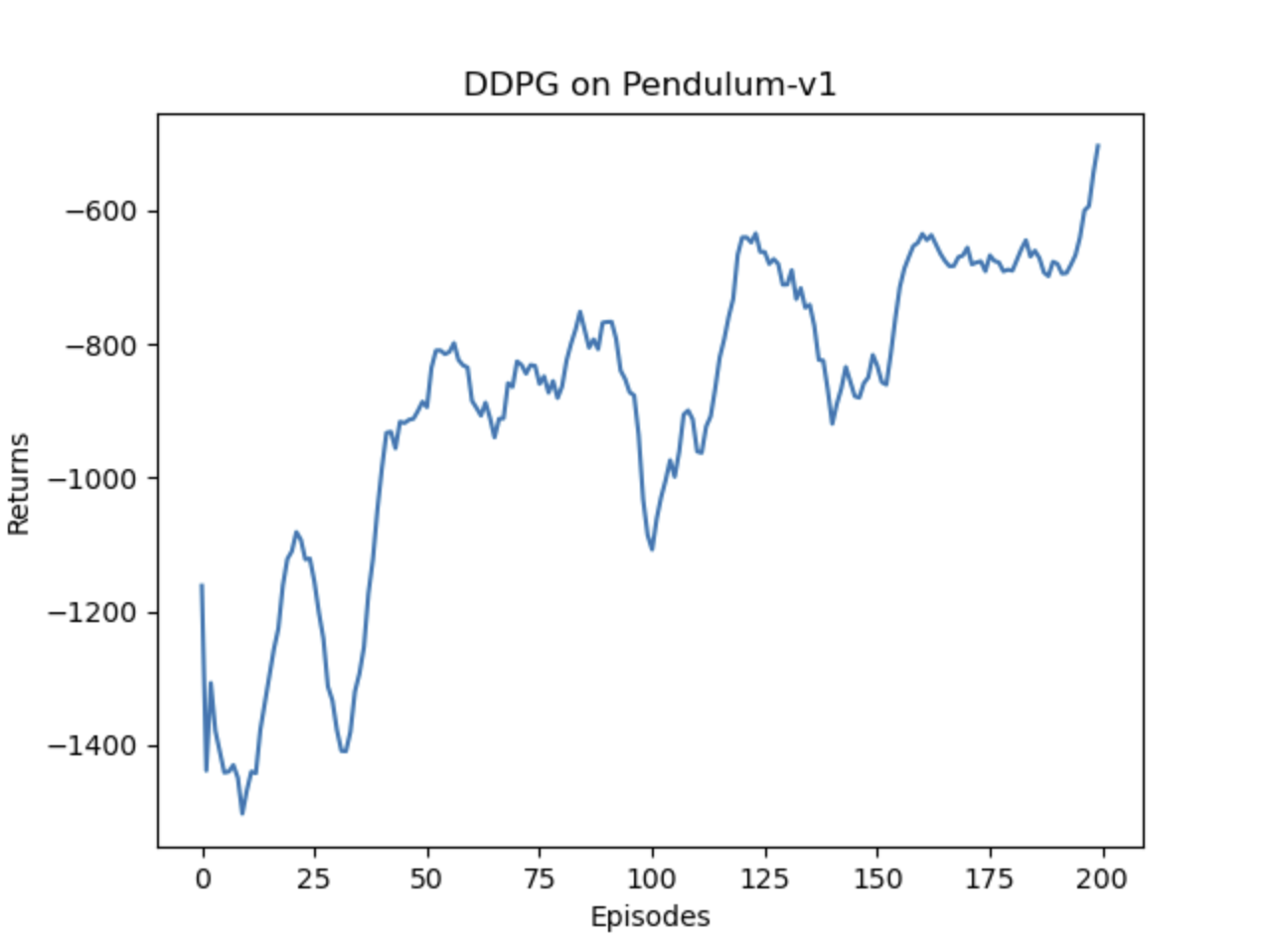
plt.show()结果
代码在 pendulum-v1环境下表现尚可,第一次跑了200轮的训练,虽然整体趋势在上升,但是奖励还是比较低的,继续训练直1000轮,可以看到模型的奖励从300轮左右开始就稳定在-200左右,总体表现良好。