创建时间: 2024年11月25日 20:29
作者: 蜡笔大新
笔记类别: 机器学习
标签: 主成分分析, 数据预处理, 线性回归
状态: 完成
简介
主成分分析(英语:Principal components analysis,缩写:PCA)是一种统计分析和简化数据集的方法。它通过正交变换将一系列可能相关的变量观测值进行线性变换,将其投影为一系列线性不相关的变量,这些不相关变量被称为主成分(Principal Components)。
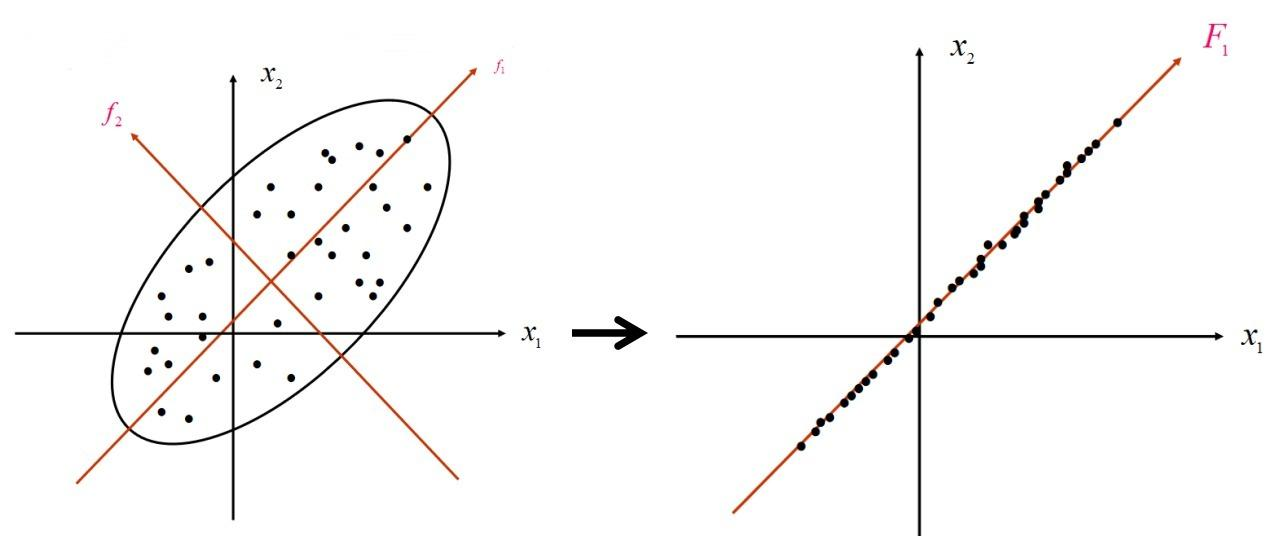
如下图所示,PCA首先确定数据的中心点,然后建立并旋转坐标系,目标是将数据点投影到坐标轴上。这个过程类似右图所示,同时要使方差最大化(即使所有点尽可能分散),从而最大程度地减少降维带来的信息损失。$f_1$ 被称为第一主成分,$f_2$ 为第二主成分,依此类推。在PCA中,k表示要保留的主成分数量,每个主成分对应一个维度方向。k值越大,降维程度越小——例如,从100维降至40维比降至2维保留了更多信息。
方差(Variance)是衡量数据分散程度的重要指标。在PCA中,我们追求投影后的数据具有最大方差,这意味着:
- 数据点在新坐标轴上分布更分散,保留了更多原始信息
- 较大的方差表示该主成分包含了更多的数据变化信息
- 通常按方差大小排序选择主成分,保留方差贡献最大的k个主成分进行降维
数学上,方差可以表示为:
Var(X) = E[(X - μ)²] === >=
# X为随机变量
# μ为X的期望值
# E为期望运算在实际应用中,我们通常通过计算各个主成分的方差贡献率和累积方差贡献率来确定需要保留的主成分个数。
具体有关的数学推导可以看这个视频:
PCA讲解
代码
本次代码环境是使用PCA的人脸识别
链接:人脸识别
# coding:utf-8
import os
from numpy import *
import numpy as np
import cv2
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['Arial Unicode MS']
# 图片矢量化
def img2vector(image):
img = cv2.imread(image, 0) # 读取图片
rows, cols = img.shape
imgVector = np.zeros((1, rows * cols))
imgVector = np.reshape(img, (1, rows * cols))
return imgVector
orlpath = "./orl_faces"
# 读入人脸库,每个人随机选择k张作为训练集,其余构成测试集
def load_orl(k):
'''
对训练数据集进行数组初始化,用0填充,每张图片尺寸都定为112*92,
现在共有40个人,每个人都选择k张,则整个训练集大小为40*k,112*92
'''
train_face = np.zeros((40 * k, 112 * 92))
train_label = np.zeros(40 * k) # [0,0,.....0](共40*k个0)
test_face = np.zeros((40 * (10 - k), 112 * 92))
test_label = np.zeros(40 * (10 - k))
# sample=random.sample(range(10),k)#每个人都有的10张照片中,随机选取k张作为训练样本(10个里面随机选取K个成为一个列表)
sample = random.permutation(10) + 1 # 随机排序1-10 (0-9)+1
for i in range(40): # 共有40个人
people_num = i + 1
for j in range(10): # 每个人都有10张照片
image = orlpath + '/s' + str(people_num) + '/' + str(sample[j]) + '.pgm'
# 读取图片并进行矢量化
img = img2vector(image)
if j < k:
# 构成训练集
train_face[i * k + j, :] = img
train_label[i * k + j] = people_num
else:
# 构成测试集
test_face[i * (10 - k) + (j - k), :] = img
test_label[i * (10 - k) + (j - k)] = people_num
return train_face, train_label, test_face, test_label
# 定义PCA算法
def PCA(data, r):#降低到r维
data = np.float32(np.mat(data))
rows, cols = np.shape(data)
data_mean = np.mean(data, 0) # 对列求平均值
A = data - np.tile(data_mean, (rows, 1)) # 将所有样例减去对应均值得到A
C = A * A.T # 得到协方差矩阵
D, V = np.linalg.eig(C) # 求协方差矩阵的特征值和特征向量
V_r = V[:, 0:r] # 按列取前r个特征向量
V_r = A.T * V_r # 小矩阵特征向量向大矩阵特征向量过渡
for i in range(r):
V_r[:, i] = V_r[:, i] / np.linalg.norm(V_r[:, i]) # 特征向量归一化
final_data = A * V_r
return final_data, data_mean, V_r
def face_recongize():
for r in range(10, 41, 10): # 最多降到40维,即选取前40个主成分(因为当k=1时,只有40维)
print("当降维到%d时" % (r))
x_value = []
y_value = []
train_face, train_label, test_face, test_label = load_orl(7) # 得到数据集
# 利用PCA算法进行训练
data_train_new, data_mean, V_r = PCA(train_face, r)
num_train = data_train_new.shape[0] # 训练脸总数
num_test = test_face.shape[0] # 测试脸总数
temp_face = test_face - np.tile(data_mean, (num_test, 1))
data_test_new = temp_face * V_r # 得到测试脸在特征向量下的数据
data_test_new = np.array(data_test_new) # mat change to array
data_train_new = np.array(data_train_new)
# 测试准确度
true_num = 0
for i in range(num_test):
testFace = data_test_new[i, :]
diffMat = data_train_new - np.tile(testFace, (num_train, 1)) # 训练数据与测试脸之间距离
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1) # 按行求和
sortedDistIndicies = sqDistances.argsort() # 对向量从小到大排序,使用的是索引值,得到一个向量
indexMin = sortedDistIndicies[0] # 距离最近的索引
if train_label[indexMin] == test_label[i]:
true_num += 1
else:
pass
accuracy = float(true_num) / num_test
x_value.append(7)
y_value.append(round(accuracy, 2))
print('当每个人选择%d张照片进行训练时,The classify accuracy is: %.2f%%' % (7, accuracy * 100))
if __name__ == '__main__':
face_recongize()
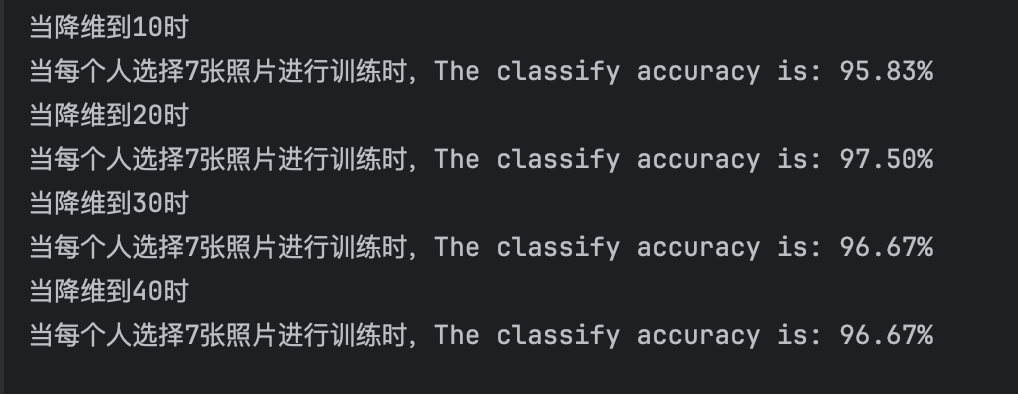
模型的准确率尚可,但是PCA降维不同维度的区别并不大,可能是由于任务较为简单。
