创建时间: 2024年11月13日 11:23
作者: 蜡笔大新
笔记类别: 强化学习
标签: 强化学习, 深度强化学习, 策略梯度算法
状态: 完成
简介
之前提到的 DQN 系列算法属于基于值函数的方法来训练模型,而 PG 系列算法则属于基于策略梯度的方法。PG 系列通常采用蒙特卡洛方法计算 G 值,并通过梯度上升更新参数。科学家们考虑将策略与时序差分(TD)方法相融合,使得无需沿着整个路径更新到结束状态再回溯就能更新当前状态。这类似于 TD 算法的思想:边前进边更新 Q 值,同时更新策略。这种方法被称为 Actor-Critic 算法。许多前沿算法都是基于 AC 进行改进的,可以说这种思想既重要又实用。与DQN的结构有些相似,AC算法也拥有两个网络,分别是Actor网络和Critic网络,接下来将分别进行介绍。
Actor网络
Actor网络负责与环境交互,并在 Critic 价值函数的指导下用策略梯度学习一个更好的策略。
Critic网络
通过 Actor 与环境交互收集的数据学习一个价值函数,这个价值函数会用于判断在当前状态什么动作是好的,什么动作不是好的,进而帮助 Actor 进行策略更新。而更新的策略则与之前的PG算法很像,都是通过梯度上升算法更新参数。
TD-Error
时序差分残差(TD-Error)是强化学习中用来衡量当前状态与预期状态的差异的指标。反映了当前状态与预期状态的差异,通常被用来更新策略网络的参数,使得策略能够更快地朝着最优策略的方向学习。
$$ \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) $$
其中:
$\delta_t$ 是在时间步 t 的TD误差
$r_t$ 是在时间步 t 获得的即时奖励
$\gamma$ 是折扣因子
$V(s_t)$ 是状态 $s_t$ 的估计值函数
$V(s_{t+1})$ 是下一个状态 $s_{t+1}$ 的估计值函数
TD-Error需要与优势函数做出一定区别。
$$ A(s, a) = Q(s, a) - V(s) $$
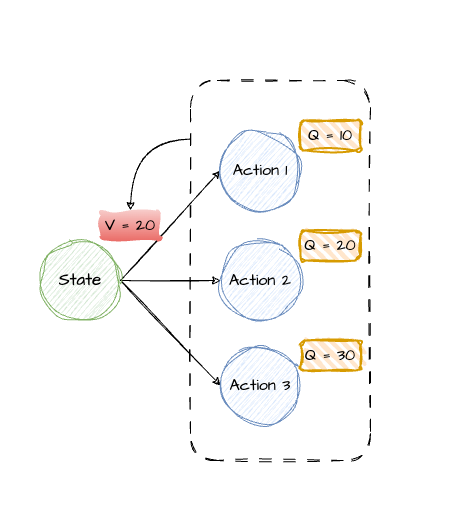
其实很好理解,Q值是执行动作的总奖励期望,而V值是到达状态后的总奖励期望(所有动作Q值的平均数),因此如果A>0,说明这个动作的期望在平均之上;反之则比平均更差。
而TD-Error的公式与优势函数其实是可以互相转化的,即 $Q=\gamma * V(S’)+r$ 。但是需要区别的是他们的含义不同。优势函数说明这个动作在该状态下是否比平均策略更优,因此是一个相对的衡量标准。
而TD-Error评价当前状态值估计与“实际“观测值的偏差。它更强调一种“矫正”效果,反映当前价值估计的准确性,并直接用于更新价值函数或策略。
更新
TD-Error: $\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$ 就可以看作“真实”值和预测值之间的差异:
- 如果 “真实”值 > 预测值(即 $\delta_t$ > 0 ),说明模型低估了当前状态的价值。为了修正这一低估,模型会增加 $V(s_t)$ 的估计值,使得预测更接近真实值。并且差得越多,更新的幅度越大。
- 如果 “真实”值 < 预测值(即 $\delta_t$ < 0 ),则模型高估了当前状态的价值。模型将减小 $V(s_t)$ 的估计值,调低预测以贴合真实值。误差越大,调整幅度也越大。
$r_t + \gamma V(s_{t+1})$ 表示更好的价值估计,因为结合了实际观测到的即时奖励和对未来价值的估计,因此实际使用时可以理解为"真实"值。
$V(s_t)$ 表示预测值:$V(s_t)$ 是模型根据当前参数对状态 $s_t$ 的价值估计。
具体而言,损失函数通常使用MSE最小化TD-Error,并通过梯度上升更新Actor的参数,通过梯度下降更新Critic的参数。实际代码中会统一使用梯度下降方便实现(给梯度上升加负号)。
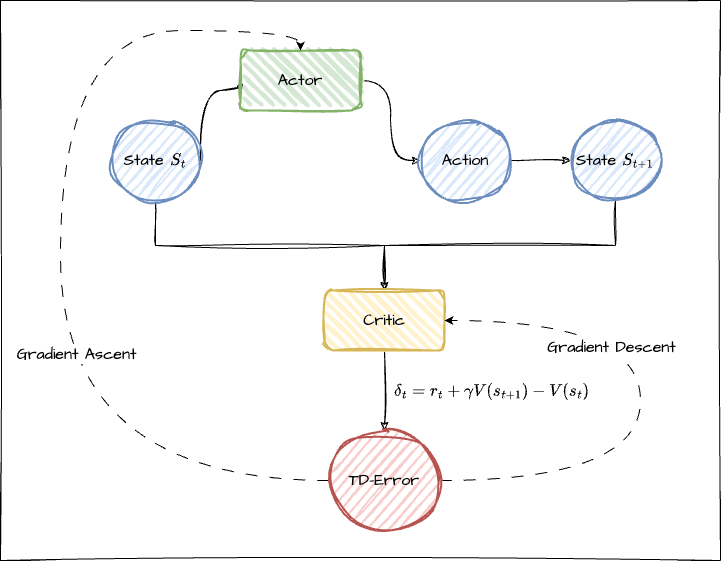
流程
Actor根据当前状态生成策略。
Actor是策略网络,它基于当前状态 $s_t$ 生成一个策略 $\pi(a|s_t)$ 。通常,策略会给出每个动作的概率分布。Actor可以:
- 选择概率最高的动作(贪婪策略)
- 根据概率分布随机采样一个动作(通常是探索时使用的方式)
执行动作,获取奖励和下一个状态。
从环境中执行Actor选出的动作 $a_t$ ,得到即时奖励 $r_t$ 和下一个状态 $s_{t+1}$ 。
Critic计算价值估计并生成TD-Error。
Critic是价值网络,通常估计状态值 $V(s)$ 。Critic网络基于当前状态 $s_t$ 和下一个状态 $s_{t+1}$ ,计算TD-Error。
Critic更新(梯度下降)。
Critic通过最小化TD-Error来更新其网络参数,即采用梯度下降更新,使得估计的状态值 $ V(s)$ 更接近真实回报。
Actor更新(梯度上升)。
Actor利用TD-Error来更新策略。TD-Error $\delta_t$ 作为一种优势信号,指导Actor优化选择动作的概率,使得策略朝着获得更高回报的方向改进。
代码
import gym
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class ValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
class ActorCritic:
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr, gamma, device):
# 策略网络
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device) # 价值网络
# 策略网络优化器
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) # 价值网络优化器
self.gamma = gamma
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
# 时序差分目标
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states) # 时序差分误差
log_probs = torch.log(self.actor(states).gather(1, actions))
actor_loss = torch.mean(-log_probs * td_delta.detach())
# 均方误差损失函数
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward() # 计算策略网络的梯度
critic_loss.backward() # 计算价值网络的梯度
self.actor_optimizer.step() # 更新策略网络的参数
self.critic_optimizer.step() # 更新价值网络的参数
actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = ActorCritic(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, gamma, device)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()
结果
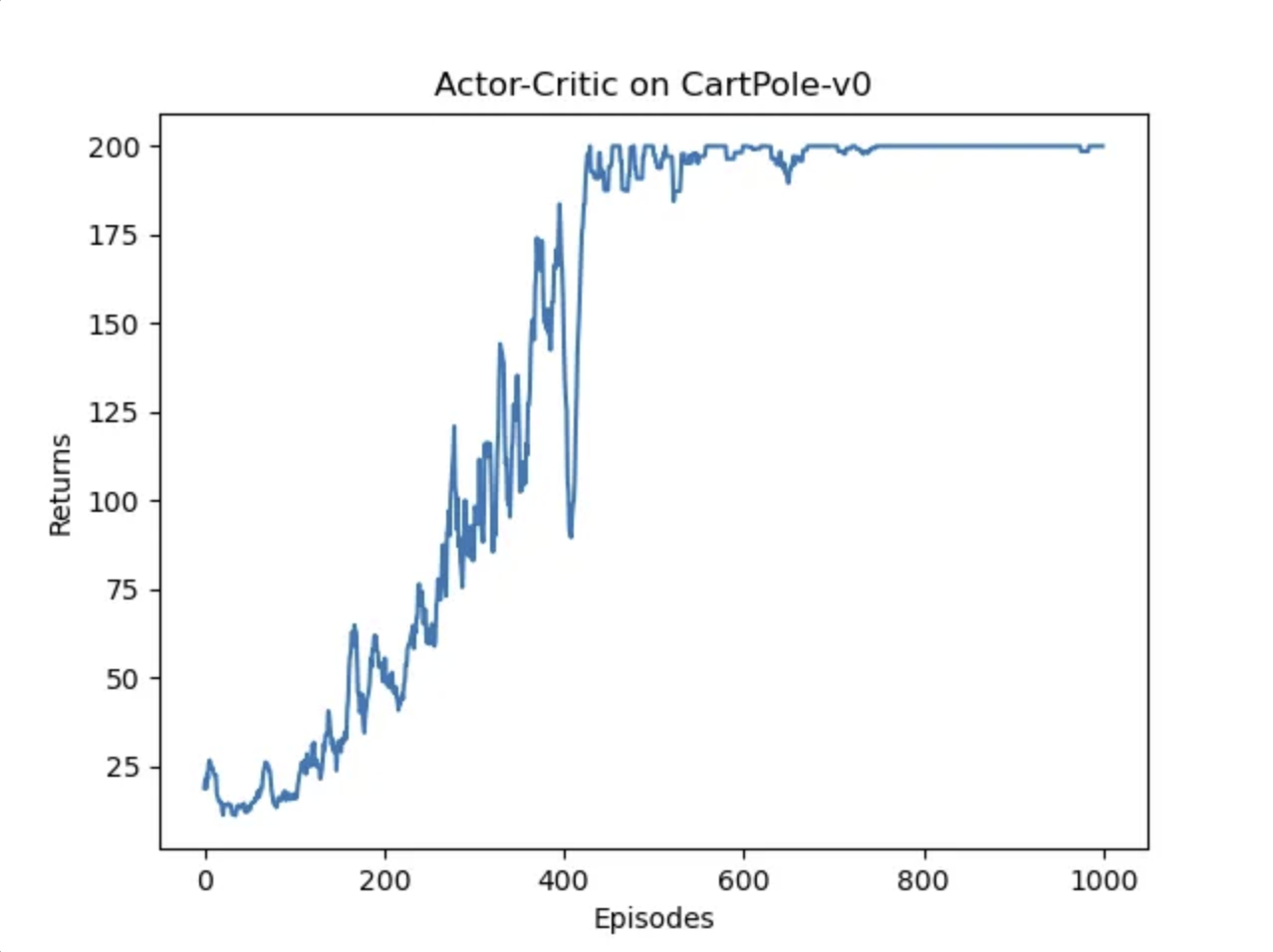
可以看出,结果还是非常不错的,相较于PG算法,震荡幅度较小,比较稳定。
