创建时间: 2024年10月28日 18:45

作者: 蜡笔大新
笔记类别: 机器学习
状态: 完成

介绍

蒙特卡洛方法（Monte Carlo Method）是一类基于随机抽样的数值计算方法，广泛用于模拟和优化问题。其核心思想是通过模拟大量随机样本，计算这些样本的统计特征来近似真实结果。

例子

求下图$[a,b]$定积分，即 $F(x)=\int_{a}^{b}f(x)dx$。

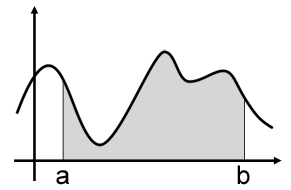
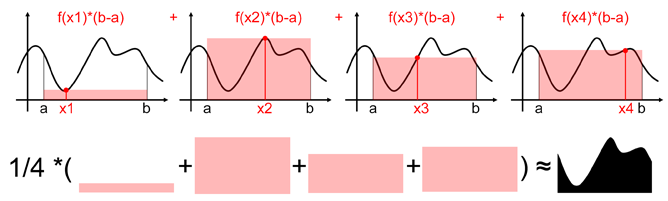
可以随机取4个x，求他们矩形的面积求平均值。即

$$ \begin{align*} S &= \frac{1}{4} (b-a) (f(x_1)+f(x_2)+f(x_3)+f(x_4))\\& = \frac{1}{4}(b-a)\sum_{i=1}^{4}f(x_i) \end {align*} $$

进一步推广，即

$$ S=\frac{1}{n}(b-a)\sum_{1}^{n}f(x_i) $$

评价

蒙特卡洛方法就是这样的思想，如果样本数量足够大，就能足够逼近真实值，但是这种方法通常也有些缺点。比如计算量较大，可能需要大量样本以确保结果准确性；结果受随机数质量影响。