创建时间: 2024年10月22日 23:53
作者: 蜡笔大新
笔记类别: 机器学习
标签: KL散度, 信息论, 熵
状态: 完成
熵的定义
热力学中表征物质状态的参量之一,其物理意义是体系混乱程度的度量。
在信息论中熵是接收的每条消息中包含的信息的平均量,消息代表来自分布或数据流中的事件、样本或特征。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。
信息量
给出信息量的定义:
$$ f(x):=信息量 $$
从信息量的角度来说,考虑踢世界杯的例子,如果中国要夺冠,那么夺冠的信息量和进入决赛+赢得决赛的信息量之和应该是一样的,即
$$ f(中国夺冠)=f(中国进决赛)+f(中国赢得决赛) $$
从概率角度来说,同时发生则应该相乘。即
$$ P(中国夺冠)=P(中国进决赛)*P(中国赢得决赛) $$
因此,信息量的定义需要满足:
$$ f(x_1*x_2)=f(x_1)+f(x_2) $$
为了满足整个体系的自洽,将信息量定义为:
$$ f(x):=-log_2x $$
为了将相加与相乘关联,很容易联想到log函数。而根据信息量的意义可知,概率越小的事情获得的信息量越大,这与生活中的常识一致,是直观的。例如国足获得世界杯冠军和阿根廷队获得世界杯冠军,显然是前者能带来更多的信息量。因此在定义信息量的时候添加负号可以显示这个特征。而选择log底数为2,则是因为与计算机有关,如果底数为2,则单位是计算机中的比特。例如概率是1/1024的事情发生了,那么信息量就是10比特。
信息熵的公式定义
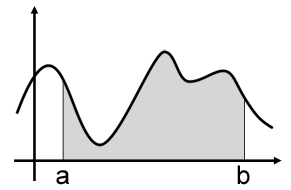
例如这样的比赛,通过公式可以计算出四个队伍赢得比赛的信息量,问题就是如何获得两场比赛各自的熵。
如果简单相加的话,显然第二场比赛熵更大。但是信息量更大的前提是中国队赢得比赛,而中国队赢得球赛的概率是1%,因此这是小概率事件,不太可能获得这么大的信息量,进而贡献给整个系统。
换个角度来说,熵代表系统的不确定性,显然第一场比赛不确定性是更高的,因此第一场比赛的熵应该大于第二场比赛。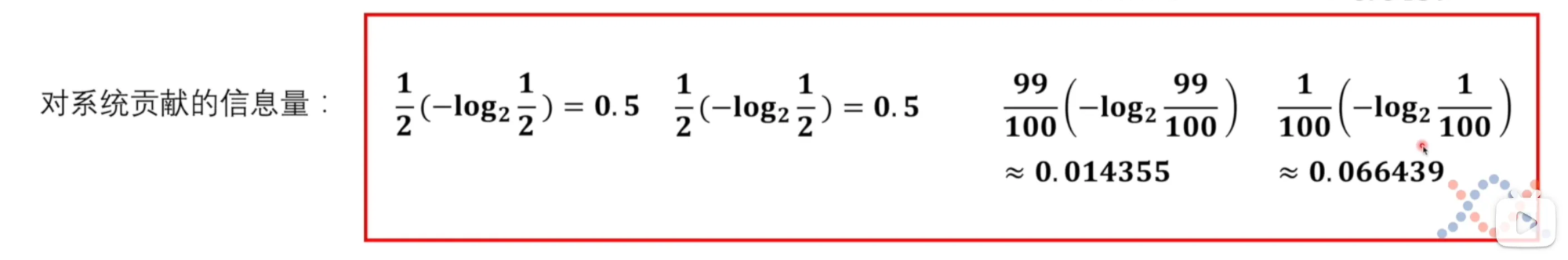
可以利用概率与信息量相乘去求熵,也就是说,熵就是信息量的期望。
$$ H(P) := E(P_f) $$
用公式推导系统熵:
$$ \sum_{i=1}^{m} p_i \cdot f(p_i) = \sum_{i=1}^{m} p_i (-\log_2 p_i) = -\sum_{i=1}^{m} p_i \cdot \log_2 p_i $$
接下来,需要一个量纲,可以定量比较两种模型的差异程度。这里就需要引入一个全新的概念——KL散度,也就是相对熵。
KL散度
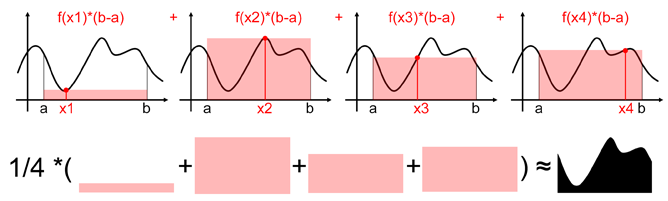
在这里可以看到P系统和Q系统两个系统的概率分布图。我们需要描述他们直接的差异,以P系统为基准,定义出P与Q的KL散度:
$$ \begin{align*}&D_{KL}(P||Q)\\ &:= \sum_{i=1}^m p_i \cdot (f_Q(q_i) - f_P(p_i)) \\ &= \sum_{i=1}^m p_i \cdot ((-\log_2 q_i) - (-\log_2 p_i)) \\ &= \sum_{i=1}^m p_i \cdot (-\log_2 q_i) - \sum_{i=1}^m p_i \cdot (-\log_2 p_i)\end{align*} $$
定义中其实就是用基准的P系统的概率乘两个系统的信息量的差值,如果P和Q系统越相似,则信息量越接近,那么KL散度就越小。继续往下推导,将信息量公式代入,将 $p_i$ 乘进去,得到两个累加式,后一个式子就是P的系统熵的公式:$\sum_{i=1}^m p_i \cdot (-\log_2 p_i)$ 。式子的前半部分,则定义为交叉熵:
$$ \begin{align*}H(P,Q) &= \sum_{i=1}^m p_i \cdot (-\log_2 q_i) \\ &= -\sum_{i=1}^m p_i \cdot \log_2 q_i \end{align*} $$
若 $\sum_{i=1}^n p_i = \sum_{i=1}^n q_i = 1$ ,且 $p_i, q_i \in (0, 1]$,则有:
$- \sum_{i=1}^n p_i \log p_i \leq - \sum_{i=1}^n p_i \log q_i$ ,等号成立当且仅当 $p_i = q_i \forall i$
证明了KL散度一定为非负数之后,也就说明如果P和Q系统相等,则KL散度为0;如果P和Q系统不相等,则一定大于0。为了让Q系统尽可能靠近P系统,我们希望KL散度尽可能小,即交叉熵尽可能小。因此交叉熵可以作为一个损失函数来衡量模型的性能(与正确模型的相似程度)。
二分类下的交叉熵公式推导(去除了1-m的求和):
$$ \begin{align*}H(P, Q) &= -\sum_{i=1,2} p_i \cdot \log_2 q_i\\& = -\sum_{i=1,2} x_i \cdot \log_2 q_i \\& = -[x \cdot \log_2 y + (1 - x) \cdot \log_2(1 - y)] \end{align*} $$
$p_i$ 可以直接由 $x_i$ 替代,代表着P系统(数据集)中的概率。 $q_i$ 并不能直接替换为 $y_i$ (模型的输出结果)。以二分类识别图片是否为猫为例, $x_i$ 表示数据集中要么是猫,要么不是猫。 $y_i$ 代表着模型认为图片为猫的概率,却没有不为猫的概率。应当同时处理 $x_i$ 是猫,模型认为是猫的情况与 $x_i$ 不是猫,模型认为不是猫的概率,因此进一步展开。
结论
虽然交叉熵和极大似然估计最后推出的结果是同一个公式,但是从推导过程来说,他们是完全不一样的。极大似然估计更多是由于log方便计算因此“凑巧”得出了这个公式。而交叉熵则是通过熵、信息量和KL散度公式推出来的。
